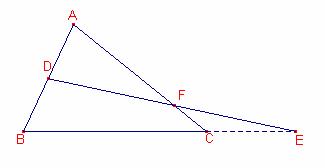
Teorema de Menelao.

Sea el triángulo , sean los puntos .

Sea la recta g que pasa por los puntos B, C. Sea el punto .

D, E, F están alineados Û

Problema 246

Propuesto por Luis Ramos Castilla (Lima, Perú)

Problema 246

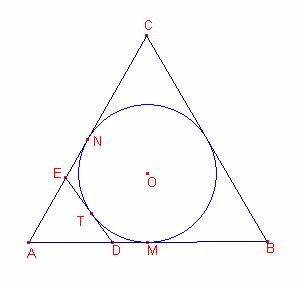
Sea ABC un triángulo equilátero y Q su circunferencia inscrita.

Sean D y E puntos de los lados AB  y AC, respectivamente, tales que DE
es tangente a Q por el arco más cercano a A

La intersección de BE y CD es U; se prolonga AU hasta cortar a BC
en R.

Demostrar que U es punto medio de AR.

Ramos L. (2005): Comunicación personal.

Solución:

Sea un triángulo equilátero .

Sea tangente a la circunferencia Q inscrita del triángulo. Sea T el punto de tangencia del segmento y la circunferencia Q.

Sean M, N puntos de tangencia de la circunferencia inscrita y el triángulo

.

,

.

Entonces el perímetro del triángulo es:

.

Sea , , Entonces, .

Aplicando el teorema del coseno al triángulo :

.

. Simplificando:

(1)

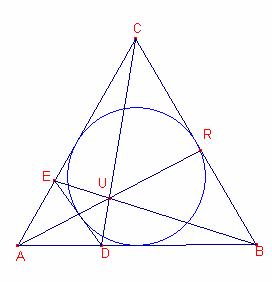
Aplicando el teorema de Menelao al triángulo :

. Entonces, (2)

Aplicando el teorema de Menelao al triángulo :

. Entonces, (3)

Sumando las expresiones (2) (3):

.

(4)

Substituyendo la expresión (1) en el denominador de la expresión (4):

.

Entonces, , por tanto U es el punto medio del segmento .