Propuesto por Luis Ramos Castilla (Lima, Perú)

Problema 246.- Sea ABC un triángulo equilátero y Q su circunferencia inscrita.

Sean D y E puntos de los lados AB  y AC, respectivamente, tales que DE es tangente a Q por el arco más cercano a A. La intersección de BE y CD es U; se prolonga AU hasta cortar a BC en R. Demostrar que U es punto medio de AR. Ramos L. (2005): Comunicación personal.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca (15 de junio de 2005)..-

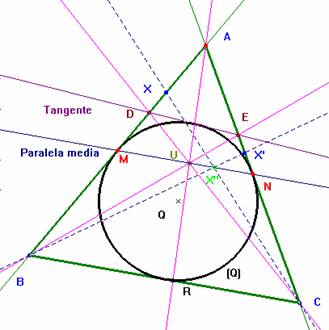
Lo que se nos pide es equivalente a demostrar que el punto U obtenido al trazar esa tangente está sobre la paralela media al lado BC. De ser eso cierto, podemos pensar que eso es válido para otras tangentes a la circunferencia. En otros términos, el procedimiento para calcular U puede utilizarse para trazar tangentes a la circunferencia. Consiste en elegir un punto en la paralela media y proyectarlo desde los vértices B y C sobre los lados opuestos. La recta unión de esas proyecciones deber ser una tangente al círculo inscrito.

Para un triángulo cualquiera ABC puede definirse la siguiente proyectividad entre las rectas AB y AC del siguiente modo:

1. A un punto X sobre AB le asocio su proyección X” sobre la paralela media MN.

2. Proyecto X” desde B sobre AC en el punto X’.

En particular, el punto A, considerado en la primera recta tiene como homólogo el punto N. Si se considera como perteneciente a la segunda, es la imagen del punto M.

Tenemos en esa homografía las imágenes de tres puntos, con los cuales podemos hallar su eje:

(A,B,M) à (N, C, A)

El eje es la recta MN, la paralela media.

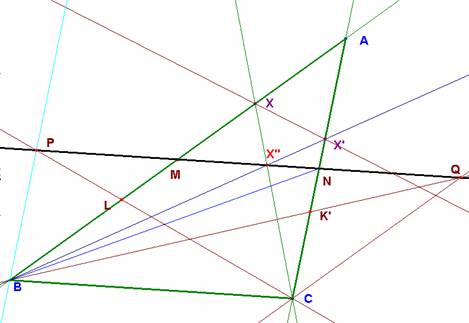
La imagen y la antiimagen del infinito se obtienen fácilmente. El punto L tiene homólogo en el infinito (se traza una paralela por B a AC y donde corte a MN ─eje de la proyectividad─ se proyecta desde C sobre AB). De modo similar se obtiene el punto K’, antiimagen del punto del infinito de AB.

Una cónica dual o tangencial se puede definir como el conjunto de rectas formadas uniendo los puntos homólogos de una proyectividad entre dos rectas. Así pues, esta proyectividad define una cónica. Queremos ver qué clase de cónica es y, en que circunstancias, coincide con la circunferencia inscrita en el triángulo.

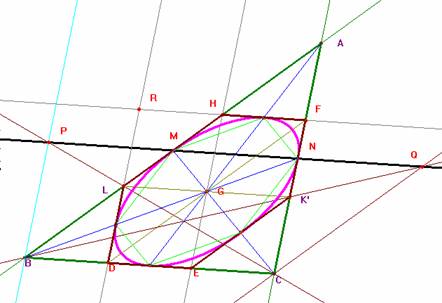
La cónica queda definida con cinco elementos. Aquí tenemos tres tangentes uniendo los tres pares de homólogos, rectas AN=AC; BC y MA=AB. Con los puntos L y K’, se obtienen las tangentes paralelas a los lados AB y AC respectivamente.

Si MN es la paralela media, los triángulos BLC y MLP son homotéticos, la razón de la homotecia que pasa del primero al segundo es –1/2, de donde concluimos que BL es igual a dos tercios de BM, o sea, es la tercera parte del lado AB. Argumento idéntico nos lleva a concluir que CK’ es igual a la tercera parte de AC.

Cuando el triángulo es equilátero, las tangentes al círculo inscrito paralelas a los lados están a un tercio del vértice y a dos tercios del lado opuesto, por tanto, la circunferencia inscrita y esta cónica tienen cinco elementos en común, los lados y las dos tangentes mencionadas. Luego son iguales como pretendíamos demostrar.

De esta cónica tangencial se pueden obtener más elementos, aunque sean innecesarios para el problema en cuestión.

Su centro es el baricentro del triángulo, pues, en cualquier cónica, los puntos de contacto de dos tangentes paralelas son un diámetro: el diámetro conjugado con la dirección de las paralelas. Su punto medio, el centro de la cónica, se encuentra pues en la paralela media. En nuestro caso, el centro está en la paralela media del trapecio ABEK’ y, dado que BD=EC=1/3 · BC, es una recta que contiene al baricentro. De igual modo, el centro se halla sobre la paralela media del trapecio ALDC y en consecuencia el baricentro es el centro de esta cónica.

Las medianas del triángulo son diámetros. La mediana CG es el diámetro conjugado con la dirección de las tangentes paralelas AB y EK’, por lo cual el punto M (pie de la mediana) es el de tangencia.

Los puntos medios de los lados del triángulo son puntos de tangencia.

Sin entrar en muchos detalles, que no se precisan para la resolución del problema, concluyamos diciendo que G además del centro es el punto de Brianchon del hexágono circunscrito a la cónica LDEK’FH, lo que implica que el hexágono formado con los puntos de tangencia, inscrito en la cónica, tienen sus lados opuestos paralelos (su recta de Pascal es la polar del punto de Brianchon, y está en el infinito)