Propuesto por Luis Ramos Castilla (Lima, Perú)
Problema 246
Sea ABC un triángulo equilátero y Q su circunferencia inscrita.
Sean D y E puntos de los lados AB y AC, respectivamente, tales que DE
es tangente a Q por el arco más cercano a A
La intersección de BE y CD es U; se prolonga AU hasta cortar a BC
en R.
Demostrar que U es punto medio de AR.
Ramos L. (2005): Comunicación personal.
Solución de Prof. William Rodriguez Chamahe.
Teorema:
Si dos triángulos tienen un par de ángulos iguales y un par de ángulos suplementarios se cumple que los lados que se oponen a los ángulos iguales y los lados que se oponen a los ángulos suplementarios son proporcionales.

Para demostrar los segmentos BC y MN los hacemos coincidir de manera que los puntos M y C también coincidan entonces obtenemos la siguiente figura

Luego prolongamos MP y por B trazamos la paralela al segmento NP que se corta en el punto T

Recuerde que M=C
Ahora aplicando el teorema de la bisectriz en el triángulo ABT:
![]()
Y como los triángulos MNP y MBT son semejantes obtenemos:
![]()
De donde se demuestra que:
![]()
Demostrar que las cuerdas que unen los puntos de tangencia de los lados de un cuadrilátero circunscrito con su incirculo, se cortan en el mismo punto con las diagonales.
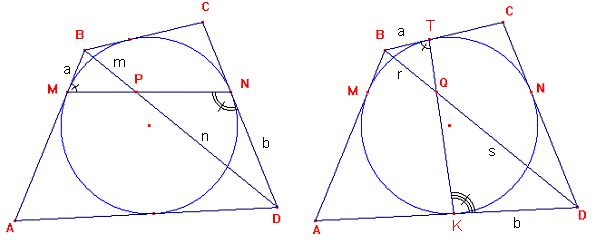
fig 246-1
Por la propiedad antes mencionada se cumple:
En los triángulos BMP y PND la siguiente relación.
![]() ………. (1)
………. (1)
Y en el triángulo BTQ y QKD se cumple la siguiente relación:
![]() ……….. (2)
……….. (2)
De las ecuaciones (1) y (2) observamos que los segmentos MN y TK cortan en la misma razón ala diagonal BD de donde concluimos que los puntos P y Q son los mismos.
De manera homologa trabajamos con la otra diagonal (AC)
Con lo que demostramos que en todo cuadrilátero las diagonales y el segmento que une los puntos de tangencia son concurrentes
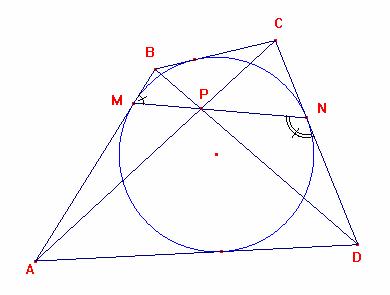
Fig 246-2
Ahora empezamos la solución al problema 246 con estas indicaciones iniciales.
En el triángulo MN es paralelo al lado BC y como M y N son puntos medios entonces el segmento MN es base media de todos los triángulos BAR por lo tanto u será punto medio de AR con lo que da demostrado que U es punto medio de AR
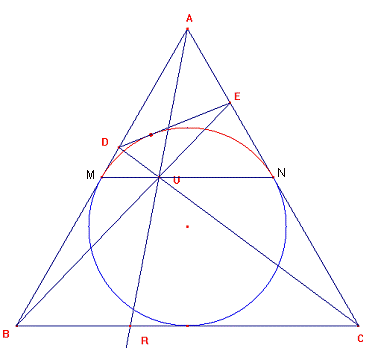
Fig 246-3
Prof. William Rodriguez Chamahe