Problema
247
(Para
el aula)
Demostrar que si H es el ortocentro del
triángulo ABC y AK es un diámetro de la circunferencia circunscrita,
entonces HCKB es un paralelogramo.
Conant, L. L. Original exercises in plane and solid geometry.
American book company,
|
|
Propuesto por
Francisco Javier García Capitán, profesor del IES Álvarez Cubero (Priego de Córdoba)
Solución
de F. Damián Aranda Ballesteros, profesor de Matemáticas
del IES Blas Infante, Córdoba (España).
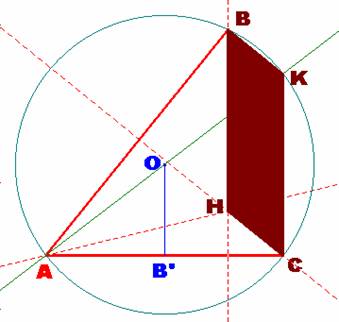
En efecto, observando la construcción realizada, vemos que
la figura BHCK es un paralelogramo, sin más que fijarnos en los lados opuestos
de dicho cuadrilátero.
En concreto, los lados CK y BH son ambos perpendiculares a una misma recta, el lado AC.
* El lado CK por ser un lado del triángulo rectángulo de catetos CK y AC e hipotenusa, el diámetro AK de la
circunferencia circunscrita al triángulo ABC.
* El lado BH es una altura del triángulo, la correspondiente al lado AC.
Por otro lado, el par de lados KB y CH son también paralelos, por
ser ambos perpendiculares a una misma recta, el lado AB.
* El lado KB por ser un lado del triángulo rectángulo de catetos AB y BK e
hipotenusa, el diámetro AK de la circunferencia circunscrita al triángulo ABC.
* El lado CH es una altura del triángulo, la correspondiente al lado AB.
En definitiva, la figura HCKB es un paralelogramo.
Además esta figura prueba que HB = CK = 2∙OB’.