La figura se traza
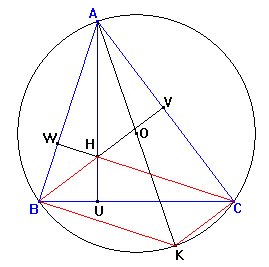
sin dificultad. | 261. Demostrar que si H es el ortocentro del triángulo ABC y AK es un diámetro de la circunferencia circunscrita, entonces HCKB es un paralelogramo. |
|
Conant, L. L. Original exercises in plane and solid geometry. Propuesto por Francisco Javier García Capitán |
Solución de Francisco Javier García Capitán
La figura se traza
sin dificultad.
Vamos a comprobar que BH es paralelo a KC y que HC es paralelo a BK.
BH es paralelo a KC
ÐHBC = ÐVBC = 90º - ÐBCV = ÐKCA - ÐBCA = ÐBCK,
HC es paralelo a BK
ÐHCB = ÐWCB = 90º - ÐCBW = ÐKBA - ÐCBA = ÐKBC.