Propuesto por Francisco Javier García Capitán ,
profesor del IES Álvarez Cubero (Priego de Córdoba)
Para el aula
Problema 247
261. Demostrar que si H es el ortocentro del
triángulo ABC y
AK es un diámetro de la circunferencia circunscrita, entonces HCKB es
un paralelogramo.
Conant, L. L. Original exercises in plane
and solid geometry
American book company,
Solución de Julio
A. Miranda Ubaldo
Profesor de
Matemáticas
Huaral (Perú) , 04 de Junio de 2005
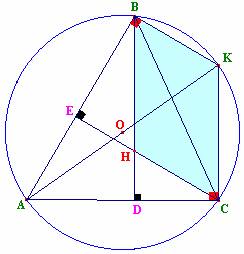
Se sabe que :
Si un lado del triángulo inscrito en una circunferencia coincide con el diámetro de ella , este triángulo es rectángulo , precisamente el diámetro viene a ser la hipotenusa del triángulo en cuestión.
En función a lo anterior :El triángulo ABK es rectángulo : AK es diámetro de la circunferencia que coincide con la hipotenusa del triángulo en cuestión , luego m Ð ABK = 90° .
Luego : BK // EC entonces BK // HC ...........(1)
Análogamente el triángulo ACK es rectángulo : AK es diámetro de la circunferencia que coincide con la hipotenusa del triángulo en cuestión , luego m Ð ACK = 90° .
Notemos que BD // KC luego BH // KC ..............(2)
De (1) y (2) se deduce que el cuadrilátero HCKB es un PARALELOGRAMO
* BD y EC son alturas del triángulo ABC , estas alturas se cortan en un punto
llamado ORTOCENTRO (H)
* “O” es el centro de la circunferencia