Propuesto por Francisco Javier García Capitán , profesor del IES Álvarez Cubero (Priego de Córdoba) Para el aula. Problema 247. 261. Demostrar que si H es el ortocentro del triángulo ABC y AK es un diámetro de la circunferencia circunscrita, entonces HCKB es un paralelogramo. Conant, L. L. Original exercises in plane and solid geometry. American book company, New York : 1905 (Pág 41)
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de junio de 2005) |
|
PLANTEAMIENTO Y SOLUCION |
|
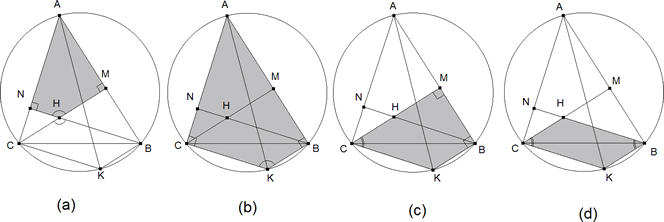
Supongamos el problema resuelto y dibujadas todas las líneas que se desprenden del enunciado. Si podemos demostrar que los ángulos opuestos del cuadrilátero HCKB son iguales dos a dos, habremos demostrado que dicho cuadrilátero es un paralelogramo.
Ver el cuadrilátero AMHN en la figura 1 (a)
Y por ser ángulos opuestos por el vértice
Ver el cuadrilátero ABKC en la figura 1 (b) Como AK es un diámetro los ángulos ABK y ACK son rectos.
Y de aquí deducimos la primera igualdad
Ver el cuadrilátero MBKC en la figura 1 (c)
Ver el cuadrilátero HBKC en la figura 1 (d)
Y de aquí deducimos la segunda igualdad
De (1) y (2) deducimos EL CUADRILATERO HBKC ES UN PARALELOGRAMO YA QUE TIENE LOS ÁNGULOS OPUESTOS IGUALES DOS A DOS |