Proposat per Francisco Javier García Capitán , professor del IES Álvarez Cubero (Priego de Córdoba)

Problema 247

261. Demostreu que si H és L’ortocentre del triangle ABC i AK es un diàmetre de la circumferència circumscrita, aleshores  HCKB és un paral·lelogram.

Conant, L. L. Original exercises in plane and solid geometry
    American book company, New York : 1905 (Pág 41)

Solució de Ricard Peiró:

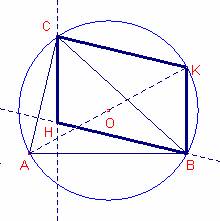Siga el triangle d’ortocentre H, inscrit en la circumferència de centre O.

Siga diàmetre de la circumferència. Aleshores, .

Per ser perpendicular a la base .

Per tant,

Per ser diàmetre .

Per ser perpendicular a la base .

Per tant, .

L’angle està inscrit en la circumferència la seua mesura és la meitat de l’arc que abraça, aleshores:

.

.

El quadrilàter CHBK és tal que els angles oposat són iguals, aleshores el quadrilàter és un paral·lelogram.