Propuesto por Francisco
Javier García Capitán , profesor del IES Álvarez
Cubero (Priego de Córdoba)
Para el aula
Problema 247
261.
Demostrar que si H es el ortocentro del triángulo ABC y
AK es
un diámetro de la circunferencia circunscrita, entonces HCKB es un
paralelogramo.
Conant, L. L.
Original exercises in plane and solid geometry
American book company, New York :
1905 (Pág 41)
Solución de Ricard Peiró:
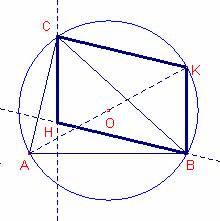Sea el triángulo
de ortocentro H,
inscrito en la circunferencia de centro O.
Siga 
diámetro de la circunferencia.
Entonces, 
.
Por ser 
perpendicular a la
base 
.
Por tanto, 
Por ser diámetro 
.
Por ser 
perpendicular a la
base 
.
Por tanto, 
.
El ángulo 
está inscrito en la circunferencia,
mide la mitad del arco que abarca, entonces:
.
.
El cuadrilátero CHBK es tal que los ángulos opuestos son iguales, entonces
el cuadrilátero es un paralelogramo.