Propuesto por Francisco Javier García Capitán , profesor del IES Álvarez Cubero (Priego de Córdoba)

Para el aula

Problema 247

261. Demostrar que si H es el ortocentro del triángulo ABC y

AK es un diámetro de la circunferencia circunscrita, entonces  HCKB es un paralelogramo.

Conant, L. L. Original exercises in plane and solid geometry
    American book company, New York : 1905 (Pág 41)

Solución:

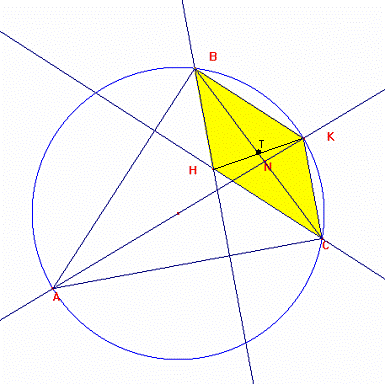
En la gráfica se demuestra que el punto T es l punto medio de HK y BC luego el cuadrilátero BHCK es un paralelogramo para mayores detalles ver en:

http://www.geometriainteractiva.com/hallasgos/demos2.htm