La herramienta
Lugar geométrico de Cabri enseguida nos muestra que el
lugar geométrico pedido es una parábola, y que el eje de dicha
parábola es la mediatriz del segmento MN.| Sean M y N los puntos medios tomados sobre dos lados cualesquiera del triángulo ABC. Sea X un punto variable elegido en el otro lado. Se pide el lugar geométrico descrito por los ortocentros cuando X se mueve sobre la recta que contiene al lado en el que se encuentra |
|
Propuesto por Juan Bosco Romero Márquez |
Solución de Francisco Javier García Capitán
Análisis con Cabri
La herramienta
Lugar geométrico de Cabri enseguida nos muestra que el
lugar geométrico pedido es una parábola, y que el eje de dicha
parábola es la mediatriz del segmento MN.
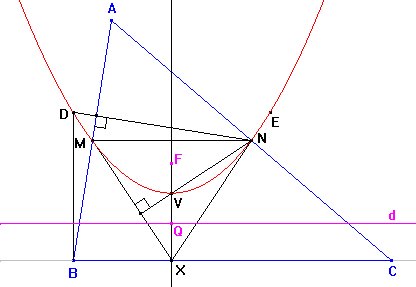
Para trazar la parábola con Cabri sin usar Lugar Geométrico, podemos considerar, como se muestra en la figura, el caso particular en que X es la intersección de BC con la mediatriz de MN. De esta manera, hallaremos el vértice V de la parábola.
En la figura, hemos trazado además el ortocentro D del triángulo BMN (haciendo X=B), y el simétrico E de D respecto de la mediatriz de MN.
Con estos cinco puntos (D, E, M, N y V) podemos usar la herramienta Cónica de Cabri y trazar nuestra parábola.
Demostración con geometría analítica
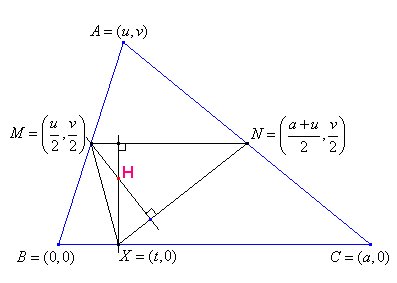Para demostrar las
afirmaciones anteriores y encontrar la ecuación y elementos de la parábola
recurrimos a la geometría analítica tomando como origen el punto
B, a C en el semieje positivo de x, y A en cualquier
lugar del plano.
Llamemos H al ortocentro del triángulo XMN. El punto H será la intersección de las recta perpendicular a BC por X (de ecuación x = t) y la perpendicular a XN por M, cuya ecuación normal es
y entonces, la intersección de las dos rectas tendrá por ecuación
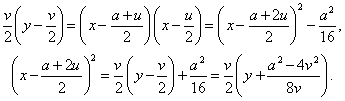
Así demostramos que se trata de una parábola, y que si la identificamos
con la fórmula general 
,
vemos que tiene 
es decir la distancia del foco al vértice es la octava parte de la altura
trazada por A al triángulo ABC.