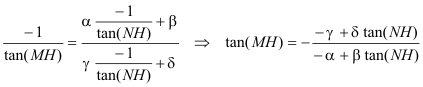Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 248

Sean M y N los puntos medios tomados sobre dos lados cualesquiera del triángulo, ABC. Sea X un punto variable elegido en el otro lado. Se pide el lugar geométrico descrito por los ortocentros cuando X se mueve sobre la recta que contiene al lado en el que se encuentra.

Romero J.B. (2005): Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de junio de 2005)

PLANTEAMIENTO - SOLUCION

TEOREMA UNO

Cuando dos haces de cuatro rectas son homográficos, si una de las rectas coincide con su imagen, las tres rectas restantes del haz cortan a sus rectas correspondientes en el otro haz en tres puntos situados en línea recta.

Podemos ver este teorema y otros con su demostración en el teorema 2.1 del problema 200 (Gergonne y el problema de Castillon) de las páginas de RICARDO BARROSO CAMPOS:

http://www.aloj.us.es/rbarroso/trianguloscabri/200extraped/gergonne.htm

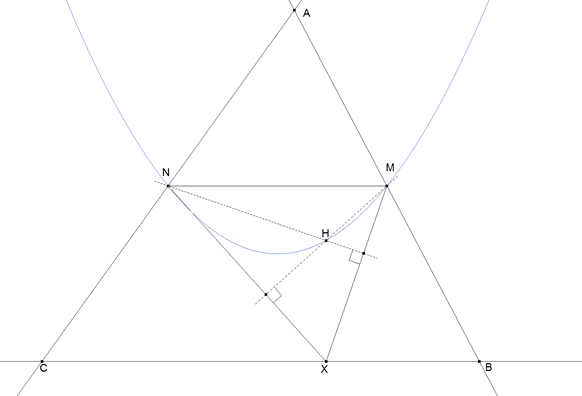
figura 1

En nuestro caso M y N son puntos fijos; por tanto podemos considerar M* y N* los haces de rectas por M y N respectivamente. Consideramos la biyección

Es claro que esta biyección es una homografía entre haces de rectas (en particular, una proyección) sólo basta recordar el teorema anterior

Si los haces M* y N* son homográficos sabemos que entre la recta MX y NX se cumple una relación algebraica del tipo

pero por definición de ortocentro

Que sustituido en la ecuación anterior

Lo que nos indica que MH y NH son homográficos y por lo tanto existe una homografía k*

Si recordamos ahora el

TEOREMA DOS (CHASLES STEINER)

La curva, lugar geométrico de los puntos de intersección de las rectas homólogas de dos haces homográficos, es una cónica que pasa por los vértices de los dos haces.

Podemos ver este teorema y otros con su demostración en el teorema 3.2 del problema 182 de las páginas de RICARDO BARROSO CAMPOS:

http://www.aloj.us.es/rbarroso/trianguloscabri/sol/sol182ped.htm

Aplicando este teorema concluimos que H describe UNA CÓNICA por M y N ya que

Si observamos que cuando x va a infinito H va a infinito y no hay más casos en lo que esto ocurra; entonces sólo hay un punto de infinito y por tanto

LA CONICA ES UNA PARABOLA

(azul en la figura 1)