Solución
con un problema previo de Ricard Peiró y Estruch profesor del IES 1 de Cheste
Problema:
Donat
el segment 
I
la recta s paral·lela a 
a una distància r.
Siga
X un punt de la recta s.
Determineu
el lloc geomètric del baricentre del triangle 
al variar X sobre la recta
s.
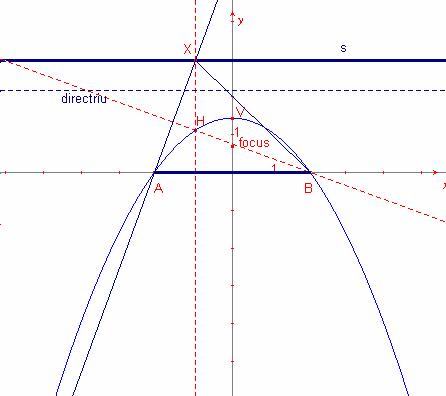
Solució:
Siga
A, B i la recta s amb les següents coordenades cartesianes:
, 
, i la recta 
.
Siga
de la recta s.
L’equació
de la recta que passa per X i és perpendicular a té equació:
L’equació
de la recta que passa per B i és perpendicular a 
té equació:
.
L’ortocentre
H és la intersecció de les rectes m, n:
.
L’ortocentre
recorre la paràbola 
Aquesta
paràbola és traslladada de la paràbola 
. És a dir 
Aleshores
la paràbola cercada té el focus en el punt 
i la directriu és la
recta 
.
Problema
248.
Proposat per Juan Bosco Romero Márquez,
professor col·laborador de
Problema
248
Siguen
M, N els punts migs de dos costats quasevol d’un triangle 
.
Siga
X un punt variable escollit sobre l’altre costat.
Determineu
el lloc geomètric dels ortocentres del triangle 
al variar X sobre la
recta que conté el costat on es troba.
Romero
J.B. (2005): Comunicación personal.
Solució:
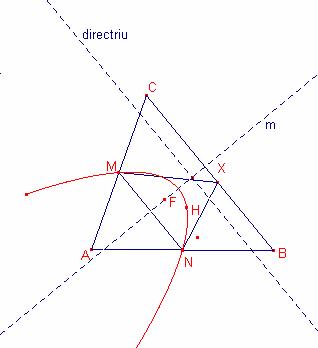
Siga
el triangle . Siga M el punt mig del costat 
. Siga N el punt mig del costat .
El
segment 
és paral·lela mitjana
del triangle .
.
Siga
X un punt sobre la recta que determina el costat 
.
Siga
altura del triangle .
La
distància entre les paral·leles , és 
.
Pel
problema anterior L’ortocentre del triangle és una paràbola que té
el focus F en la mediatriu m del segment a una distància 
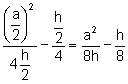del segment i la directriu
perpendicular a la mediatriu m a una distància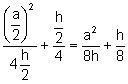 
del segment .