Solución
con un problema previo de Ricard Peiró y Estruch profesor del IES 1 de Cheste
Problema:
Dado el segmento 
y la recta s paralela
a 
a una distancia r.
Sea X un punto de la recta s.
Determina el lugar geométrico del baricentro del triángulo 
al variar X sobre la
recta s.
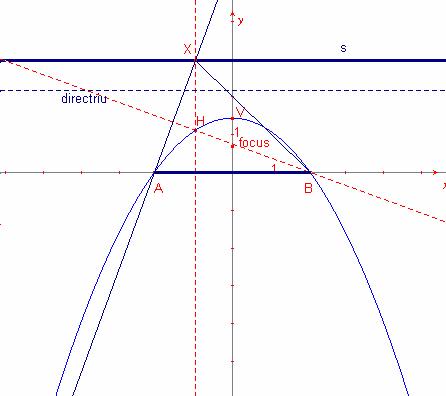
Solución:
Sea A, B y la recta s con leas siguientes coordenadas cartesianas:
, 
, i
la recta 
.
Sea 
de la recta s.
La ecuación de la recta que pasa por X y es perpendicular a tiene ecuación:
La ecuación de la recta que pasa por B y es perpendicular a 
tiene ecuación:
.
El ortocentro H es la intersección de las rectas
m, n:
.
El ortocentro recorre la parábola 
Esta parábola es trasladada de la parábola 
. Es decir 
Entonces la parábola buscada tiene el foco en el punto 
y la directriz es la
recta 
.
Problema 248.
Propuesto por Juan Bosco Romero Márquez, profesor
colaborador de
Problema 248
Sean M y N los puntos medios tomados sobre dos lados cualesquiera del triángulo, ABC.
Sea X un punto variable elegido en el otro lado.
Se pide el lugar geométrico descrito por los ortocentros
cuando X se mueve sobre la recta que contiene al lado en el que se encuentra
Romero J.B. (2005): Comunicación personal.
Solución:
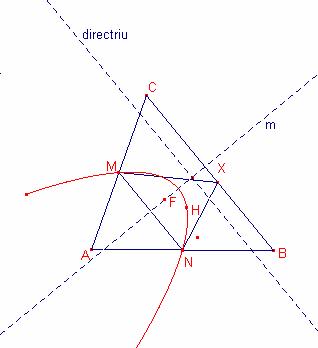
Siga el triángulo 
. Siga M el punto medio del lado 
. Siga N el punto medio del lado .
El segmento 
es paralelo a la mediana
del triángulo .
.
Sea X un punto sobre la recta que determina el lado 
.
Sea 
altura del triángulo .
La distancia entre las paralelas , es 
.
Por el problema anterior el ortocentro del
triángulo 
es una parábola que
tiene el foco F en la mediatriz m del segmento a una distancia 
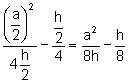del segmento y la directriz
perpendicular a la mediatriz m a una distancia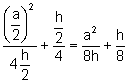 
del segmento .