Propuesto por Juan Bosco Romero Márquez,
profesor colaborador de
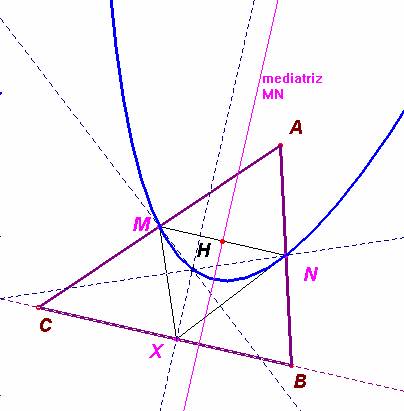
Problema 248.- Sean M y N los
puntos medios tomados sobre dos lados cualesquiera del triángulo, ABC. Sea X un
punto variable elegido en el otro lado.
Se pide el lugar geométrico descrito por los ortocentros cuando X se mueve sobre la recta que contiene
al lado en el que se encuentra.
Romero J.B. (2005): Comunicación personal.
Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.-
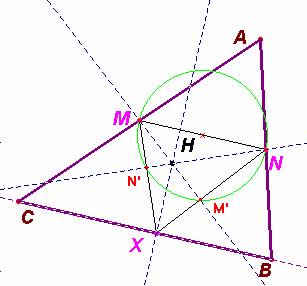
Para toda recta que pase por M hay una única perpendicular a ella que pasa por N. Esta última corta a BC en el punto X, con lo que se puede hallar una única recta que pasa por N y es perpendicular a MX. Con esto se prueba que toda recta de M* (haz de rectas que pasa por M) es la altura de algún triángulo MNX y que la correspondencia establecida entre los haces M* y N* es una proyectividad.
La concreción de esta correspondencia es como sigue:
· Tomo una recta cualquiera MH de M*
· Cortamos con la circunferencia de diámetro MN y le asocio la proyección de su corte M’ desde N (recta NX ).
· Corto con BC (punto X) y proyecto desde M ( recta MX)
· Cortamos con la circunferencia de diámetro MN y le asocio su proyección desde N (recta NN’)
Como los puntos de intersección de los pares de rectas homólogas en una proyectividad entre haces es una cónica, la conclusión de todo esto es que el lugar geométrico pedido es una cónica. Ahora vamos a ver de qué tipo de cónica se trata.
El segmento MN es paralelo a la base BC, toda recta perpendicular a ella puede considerarse la altura de algún triángulo MNX y por tanto contiene un único ortocentro sobre ella. Todas estas rectas contienen un punto de la cónica buscada, como una cónica y una recta se cortan en dos puntos, el otro ha de estar en el infinito. La única cónica posible con un haz de rectas paralelas que sólo la cortan en un punto es una parábola. Todas esas rectas son los diámetros de la misma.
Ya que los vértices M y N de la correspondencia entre haces que define la cónica pertenecen a ella, la mediatriz de MN es el eje de simetría de la parábola de los ortocentros.
Finalmente, si el segmento MN no es paralelo a la base, la solución no cambia esencialmente: todas las rectas perpendiculares a él, contienen un punto de la cónica, un ortocentro. Se trata igualmente de una parábola.