Problema 249

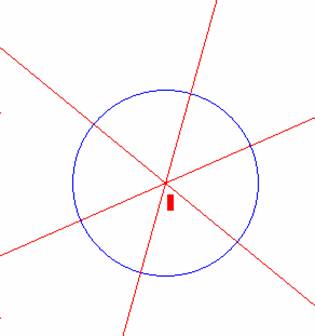
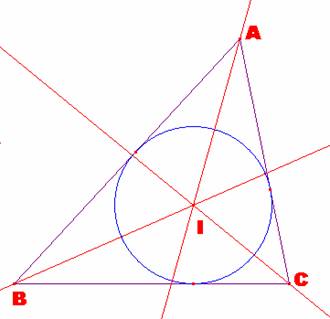
Circunscribir un triángulo a un círculo de manera que los tres vértices estén sobre tres rectas que pasan por el centro del círculo.

Sapiña, J. (1955): Problemas Gráficos de Geometría, Litograf. Madrid.
(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor ).
Propuesto por José María Pedret, Ingeniero Naval (Esplugues de Llobregat, Barcelona)

Solución de F. Damián Aranda Ballesteros, profesor de Matemáticas
del IES Blas Infante, Córdoba (España).

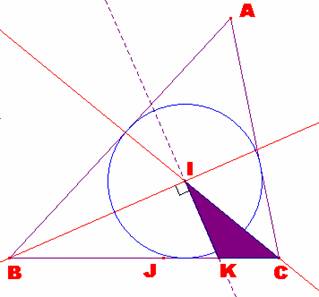
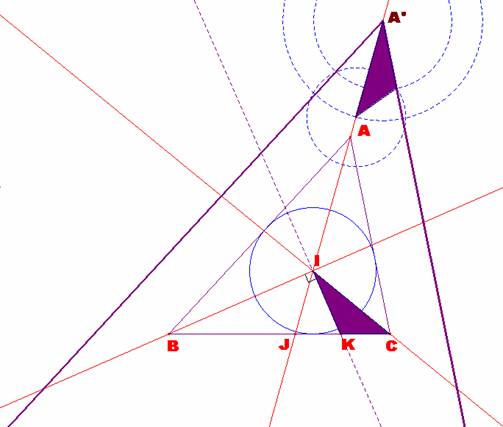
	Analizando la figura ya resuelta, observamos unas relaciones entre ángulos que dan luz a este ingenioso problema. El ángulo Ð JIC = ÐA/2 +ÐC/2 El ángulo Ð JIB = ÐA/2 +ÐB/2 Por tanto, el ángulo Ð BIC = ÐA +ÐC/2+ÐB/2 = Ð90º +ÐA/2. En definitiva, podemos construir el ángulo ÐA/2 sin más que restar 90º al ángulo Ð BIC , como se ve en la siguiente ventana.
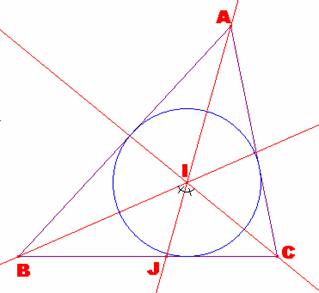
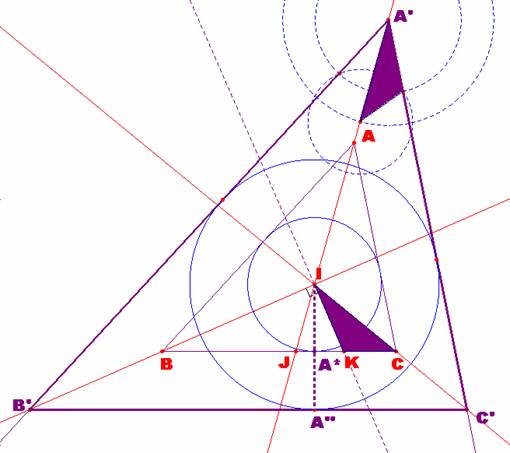
	De igual modo, podríamos construir el ángulo mitad de B y C, aunque bastaría con la construcción de uno sólo de ellos. Una vez que hemos construido uno cualquiera de los ángulos mitad de los iniciales A, B o C, continuamos ahora trasladando mediante la herramienta compás dicho ángulo sobre la semirrecta IA’, eligiendo como A’ un punto cualquiera de ella. Véase la siguiente ilustración.

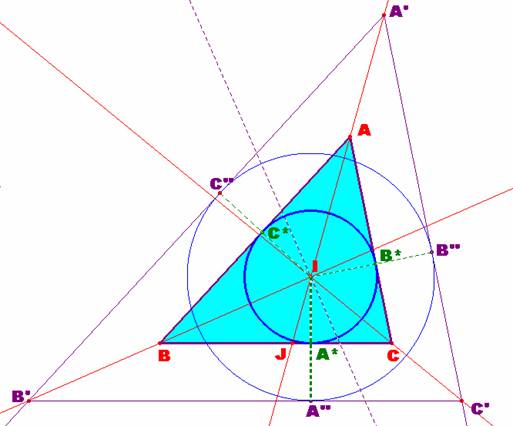
Así de esta forma podemos trazar sendas semirrectas desde el punto A’ que al interceptar a las otras dos rectas dadas, determinan los vértices B’ y C’, respectivamente. Este triángulo será homotético al solicitado, con el centro de homotecia en el incentro I.
A partir de esta semejanza, determinamos la circunferencia inscrita correspondiente al triángulo A’B’C’ y sus puntos de contacto, A’’B’’C’’ con el triángulo que serán los puntos imagen por aquella homotecia respecto del triángulo solicitado. Una vez hallados estos puntos de contacto, la construcción final del triángulo ABC no supone dificultad alguna.