Problema 249 de triánguloscabri
| Circunscribir un triángulo a un círculo
de manera que los tres vértices estén sobre tres rectas que
pasan por el centro del círculo. |
Problemas Gráficos de Geometría de Juan
Sapiña Borja. Propuesto por Jose María Pedret
|
Solución de Francisco
Javier García Capitán
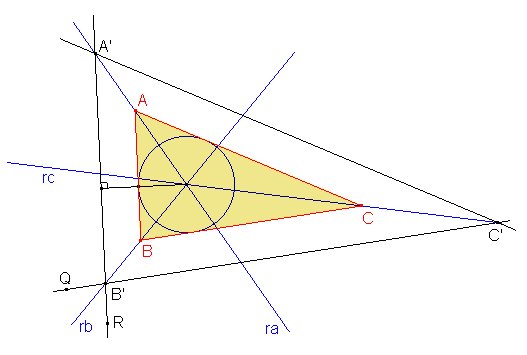 Despreocupémonos
del círculo y consigamos primero un triángulo A'B'C' que
tenga por bisectrices a las tres rectas dadas. Para ello, sea A' cualquier
punto sobre ra, una de las rectas, y sean P el simétrico
de A' respecto de rc, y R el simétrico de Q respecto
de rb. La recta A'R será la recta A'B', por lo que
B' aparece como intersección de A'R y rb.
Despreocupémonos
del círculo y consigamos primero un triángulo A'B'C' que
tenga por bisectrices a las tres rectas dadas. Para ello, sea A' cualquier
punto sobre ra, una de las rectas, y sean P el simétrico
de A' respecto de rc, y R el simétrico de Q respecto
de rb. La recta A'R será la recta A'B', por lo que
B' aparece como intersección de A'R y rb.
La recta B'C' es la simétrica de A'B' respecto de rb.
La intersección de esta recta simétrica con rc nos dará
el tercer vértice C'.
La circunferencia inscrita al triángulo A'B'C' será concéntrica
a la circunferencia dada, así que todo lo que hay que hacer es aplicar
al triángulo A'B'C' la homotecia que lleva una circunferencia
en la otra. Para ello, trazamos una perpendicular a A'B' por el centro
de la circunferencia dada, hallamos el punto de intersección de esta
perpendicular con la circunferencia, y trazamos por ella una paralela a A'B'
que determinará los vértices A y B al cortar con
ra y rb. los lados AC y BC se obtienen trazando
paralelas a A'C' y B'C' respectivamente.
 Despreocupémonos
del círculo y consigamos primero un triángulo A'B'C' que
tenga por bisectrices a las tres rectas dadas. Para ello, sea A' cualquier
punto sobre ra, una de las rectas, y sean P el simétrico
de A' respecto de rc, y R el simétrico de Q respecto
de rb. La recta A'R será la recta A'B', por lo que
B' aparece como intersección de A'R y rb.
Despreocupémonos
del círculo y consigamos primero un triángulo A'B'C' que
tenga por bisectrices a las tres rectas dadas. Para ello, sea A' cualquier
punto sobre ra, una de las rectas, y sean P el simétrico
de A' respecto de rc, y R el simétrico de Q respecto
de rb. La recta A'R será la recta A'B', por lo que
B' aparece como intersección de A'R y rb.