Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)
Problema 249 341 Circunscribir un triángulo a un círculo de manera que los tres vértices estén sobre tres rectas que pasan por el centro del círculo.
Sapiña, J. (1955): Problemas Gráficos de Geometría,Litograf. Madrid. (Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de junio de 2005) |
|
PLANTEAMIENTO Y PROBLEMA AUXILIAR |
|
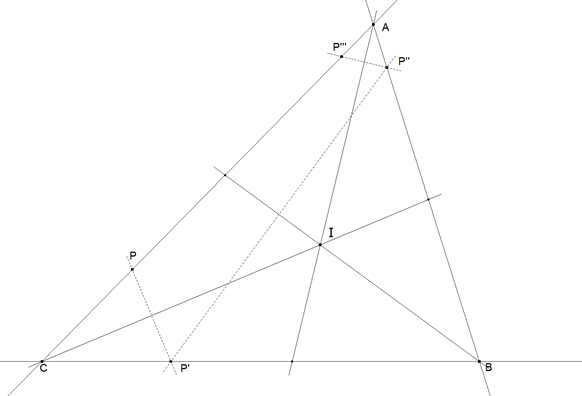
“... Construir un triángulo conociendo, en posición, sus tres bisectrices y un punto sobre el perímetro del triángulo ...”
Supongamos este problema resuelto
figura 1
Sea P el punto sobre el perímetro, en particular el lado CA. El simétrico de P respecto a la bisectriz de C es P’ que está sobre BC. El simétrico de P’ respecto a la bisectriz de B es P’‘ que está sobre AB. El simétrico de P’‘ respecto a la bisectriz de A es P’‘’ que está sobre CA. La recta CA coincide con la recta PP’‘’ y por lo tanto será
Por lo tanto dados P, CI, BI, AI; si obtenemos por simetrías sucesivas P, P’, P’‘, P’‘’ somos capaces de hallar A, B, C.
EN NUESTRO ENUNCIADO INICIAL NO TENEMOS ESTE PUNTO P; PERO SÍ SABEMOS QUE CUALQUIER TRIÁNGULO HOMOTÉTICO AL DADO, TENDRÍA LAS MISMAS BISECTRICES.
Visto lo anterior, partiremos de un punto P CUALQUIERA y obtendremos un triángulo homotético al pedido. A partir de este y gracias al círculo que nos dan hallaremos el triángulo pedido.
|
|
SOLUCION |
|
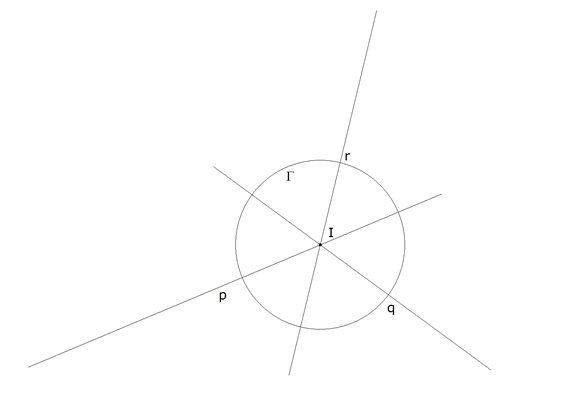
PASO I enunciado
figura 2
Sea Γ el círculo dado de centro I; sea p la recta por I que contiene a C; sea q la recta por I que contiene a B y sea r la recta por I que contiene a A.
|
|
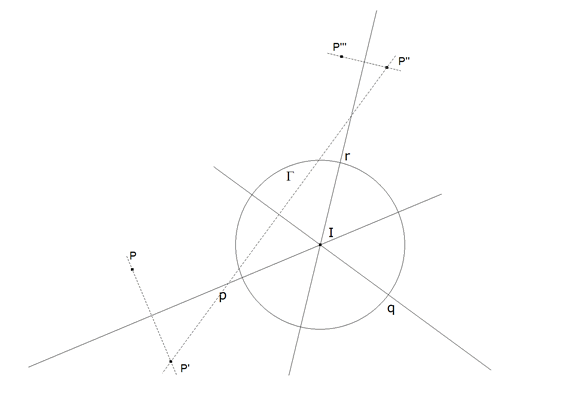
PASO II puntos simétricos
figura 3
Recordemos ahora la técnica del problema auxiliar. Tomamos un punto P cualquiera y obtenemos P’ el simétrico de P respecto a p; P’‘ el simétrico de P’ respecto a q y P’‘’ el simétrico de P’‘ respecto a r.
|
|
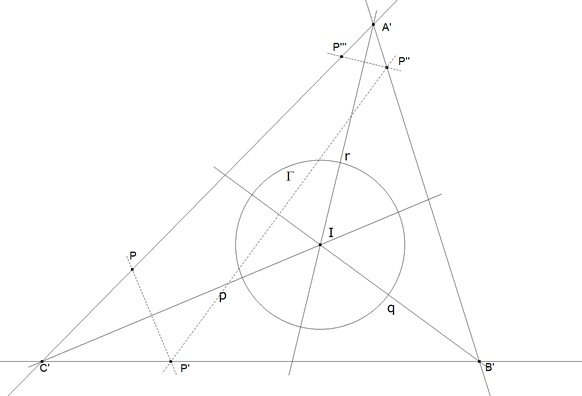
PASO III el triángulo homotético al buscado
figura 4
Seguimos con la técnica del problema auxiliar.
A’B’C’ es un triángulo homotético al buscado.
|
|
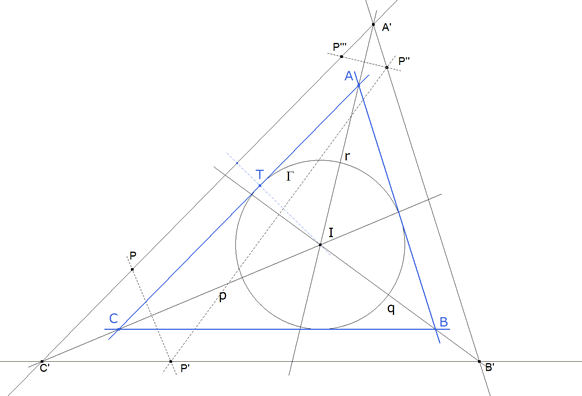
PASO IV el triángulo buscado
figura 5
Trazamos por I una perpendicular a C’A’ que corta a Γ en T que será el punto de tangencia con CA que a su vez debe ser paralelo a C’A’.
Por T una paralela a C’A’ que corta a p en C y a r en A.
Por C una paralela a B’C’ que corta q en B. Con AB cerramos el triángulo.
ABC es el triángulo buscado (azul en la figura).
|