Propuesto por José María Pedret, enginyer naval (Esplugues de Llobregat, Barcelona)

Problema 249

341

Circumscriure un triangle a un cercle de forma que els tres vèrtexs estiguen sobre tres rectes que passen pel centre del cercle.

Sapiña, J. (1955): Problemas Gráficos de Geometría,Litograf. Madrid.

(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solució:

Suposem el problema resolt.

Siga el triangle que té I per incentre i les tres rectes (1, 2, 3) bisectrius.

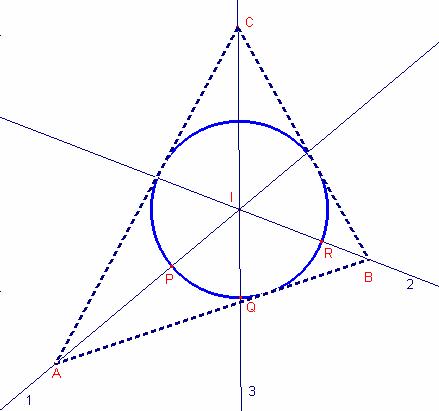
Siga x l’angle que formen les rectes 1 i 3, .

Siga y l’angle que formen les rectes 2 i 3, .

Siga , .

Aleshores, ,

Per tant, , .

Dibuixarem un triangle qualsevol amb els angles anteriors.

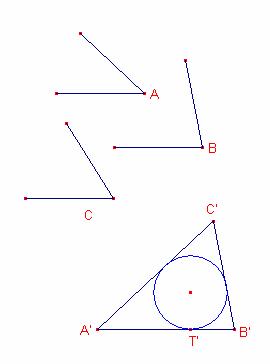
Después he construït un triangle igual a l’alterior que tinga l’incentre I i les mateixes bisectrius que el que busquem.

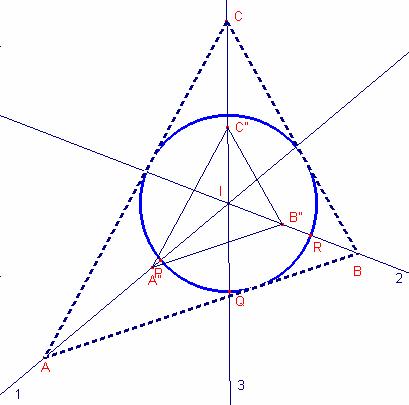
He dibuixat la circumferència inscrita a l’anterior i he dibuixat el punt de tangencia T”.

He dibuixat la recta IT” que talla la circumferència inicial en T punt de tangencia del triangle inicial i la circumferència inscrita.

He dibuixat el triangle .

Solució amb CABRI:

Figure barroso249.fig

Applet created on 2/06/05 by Ricard Peiró with CabriJava