Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)

Problema 249

341

Circunscribir un triángulo a un círculo de manera que los tres vértices estén sobre tres rectas que pasan por el centro del círculo.

Sapiña, J. (1955): Problemas Gráficos de Geometría,Litograf. Madrid.

(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Primeramente trataremos de demostrar que los segmentos NP y MX son perpendiculares siendo M, N y P las intersecciones de las bisectrices con la circunferencia inscrita además observamos que X es punto de tangencia con uno de los lados del triángulo circunscrito.

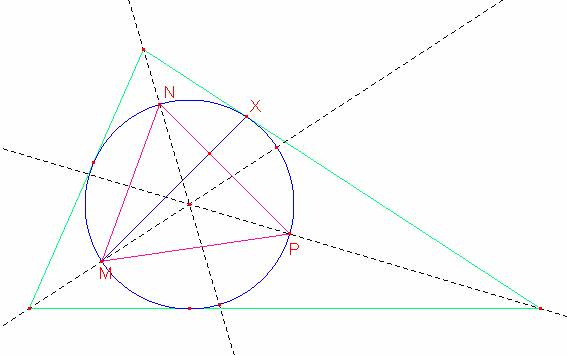
Demostración:

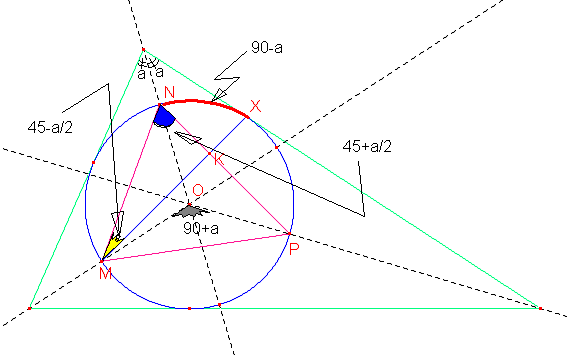
En el grafico observamos que el (ángulo formado por dos bisectrices interiores)

Luego el

Por otro lado sabemos que el arco NX=90-a

Por lo tanto el

Finalmente el triángulo MNK es rectángulo recto en K

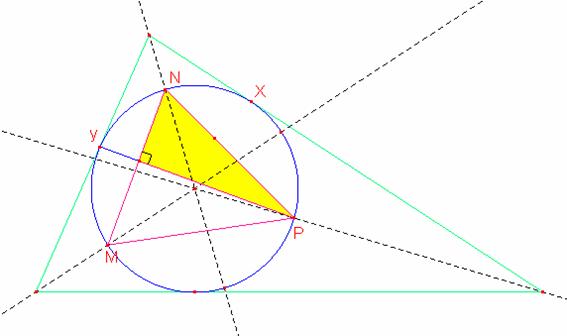
Ahora para calcular los demás punto de tangencia trabajamos de manera homologa

Siendo estas las graficas

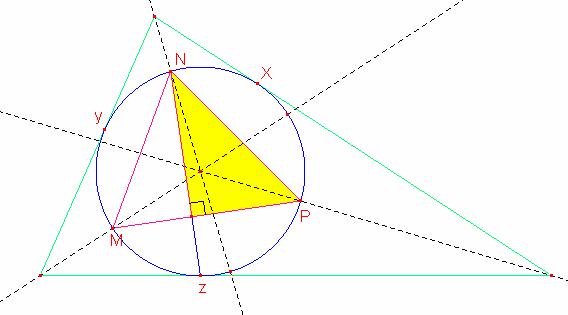
Ahora procederemos ala construcción del problema.

Sea C1 la circunferencia dada y L1, L2 y L3 las rectas que pasan por el centro del círculo dado

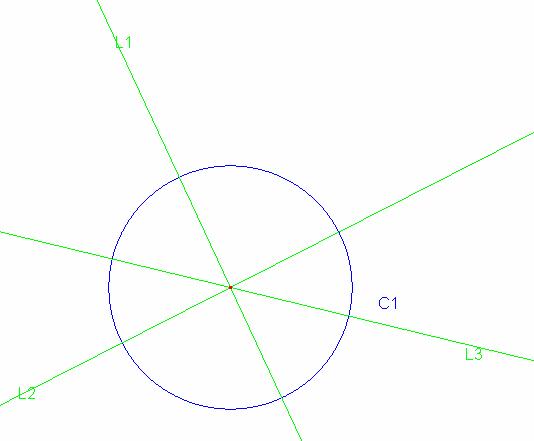
Definitivamente las rectas dadas serán las bisectrices de los ángulos del triángulo circunscrito luego estas bisectrices cortan a la circunferencia en los puntos M, N y P

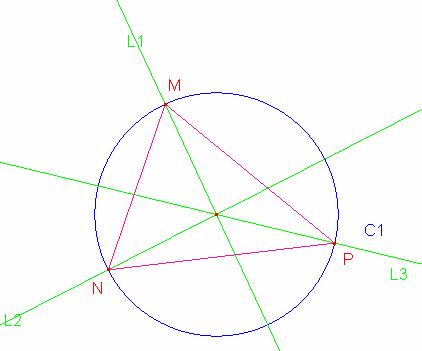
Luego trazamos las alturas del triángulo MNP cortando a la circunferencia en los puntos X, Y y Z

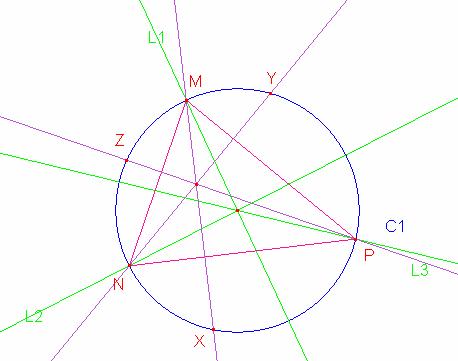
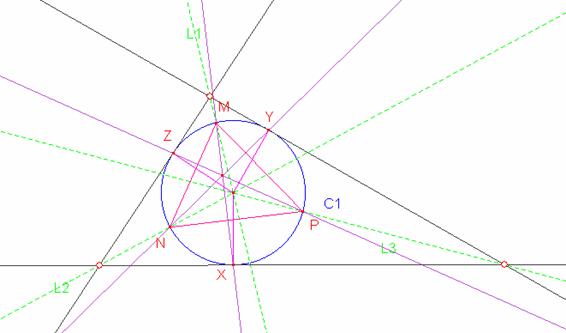
Siendo estos puntos los puntos de tangencia del triángulo circunscrito a la circunferencia dada

Entonces trazamos por los puntos X, Y y Z las tangentes a la circunferencia determinándose los vértices del triángulo en y ubicados cada uno sobre las retas dadas

Prof. William Rodríguez Chamache