 Es conocido que las
rectas que unen los vértices A, B, C con los puntos
M, N y P de contacto de los círculos exinscritos
concurren en un punto, llamado punto de Nagel del triángulo ABC.
Es conocido que las
rectas que unen los vértices A, B, C con los puntos
M, N y P de contacto de los círculos exinscritos
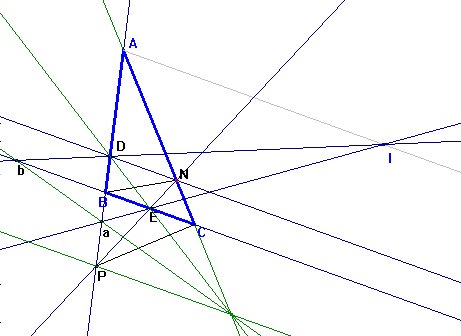
concurren en un punto, llamado punto de Nagel del triángulo ABC.| En un triángulo ABC se toman los puntos M, N y P de contacto de los círculos exinscritos en los ángulos A, B y C con los lados BC, CA y AB respectivamente. Se une N con M y con P, cortando la recta NM a AB en D, y la NP a BC en E y se designa por I el punto de encuentro de BN y CP. Siendo a el punto común de IE y AB, y b el de intersección de ID con BC, demostrar que las rectas AN, PM, DE y ab concurren en un mismo punto |
|
Instituto Jorge Juan. Propuesto por Maite Peña Alcaraz |
Solución de Francisco Javier García Capitán
Resolveremos una generalización del problema con coordenadas baricéntricas. Aplicando el resultado obtenido al caso particular planteado por el problema deduciremos que las cuatro rectas son paralelas cuando el triángulo es isósceles en B.
 Es conocido que las
rectas que unen los vértices A, B, C con los puntos
M, N y P de contacto de los círculos exinscritos
concurren en un punto, llamado punto de Nagel del triángulo ABC.
Es conocido que las
rectas que unen los vértices A, B, C con los puntos
M, N y P de contacto de los círculos exinscritos
concurren en un punto, llamado punto de Nagel del triángulo ABC.
Vamos a comprobar que el enunciado del problema es cierto en el caso general de que AM, BN y CP sean tres cevianas concurrentes en un punto cualquiera I.
En efecto, tendremos las coordenadas baricéntricas I=(u:v:w), M=(0:v:w), N=(u:0:w) y P=(u:v:0).
Entonces podemos calcular las rectas
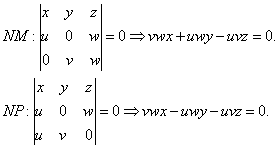
Haciendo z=0 en NM obtenemos D =(-u:v:0), y haciendo x=0 en NP obtenemos E=(0:v:-w).
Evidentemente es I=(u:v:w). Entonces podemos calcular las rectas
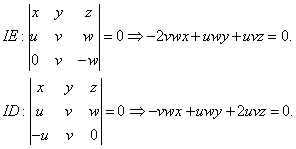
Como intersección de IE y AB resulta el punto a=(u:2v:0),
Como intersección de ID y BC resulta el punto b=(0:2v:w).
Hay que comprobar que las rectas
son concurrentes. Es evidente que las cuatro pasan por el punto pasan por el punto (u:0:-w).
Observación: Este punto común a todas las rectas será un punto del infinito, siendo paralelas las cuatro rectas, si u-w =0. En el caso del enunciado del problema tenemos que (u:v:w)=(s-a:s-b:s-c) que será un punto del infinito si y solo si a=c, es decir si el triángulo es isósceles en B.