Propuesto por Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid).
EJERCICIOS PROPUESTOS: 625. En un triángulo ABC se toman los puntos M, N y P de contacto de los círculos exinscritos en los ángulos A, B y C con los lados BC, CA y AB respectivamente. Se une N con M y con P, cortando la recta NM a AB en D, y la NP a BC en E y se designa por I el punto de encuentro de BN y CP.
Siendo a el punto común de IE y AB, y b el de intersección de ID con BC, demostrar que las rectas AN, PM, DE y ab concurren en un mismo punto.
Espeso, G. (1947) MATEMATICA ELEMENTAL Revista publicada por el instituto Jorge Juan de matemáticas y la Real Sociedad Matemática Española
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (3 de junio de 2005) |
|
PLANTEAMIENTO |
|
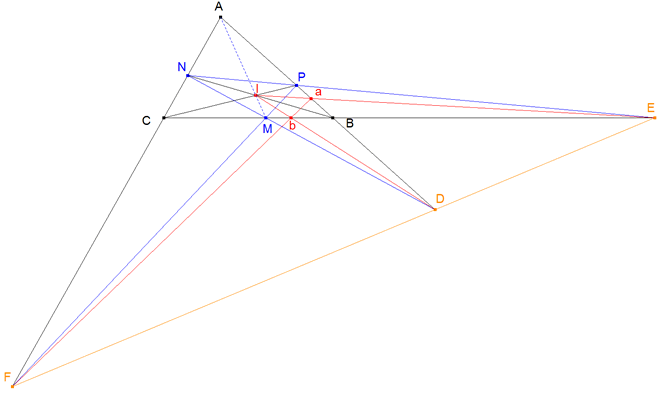
Ejecutamos, en primer lugar, el trazado de la figura que se desprende del enunciado. Dibujamos algunas rectas y puntos en colores distintos para diferenciarlas mejor y también para agruparlas convenientemente. Estudiamos entonces la figura que sigue.
Las líneas negras son los lados del triángulo dado. Las líneas azules son las formadas por el triángulo que tiene como vértices los puntos de contacto. Es claro pues que I es el punto de Nagel del triángulo ABC. Las líneas rojas son las del triángulo que se construye a partir de I según el enunciado.
Hemos identificado por tanto tres triángulos distintos
ABC MNP abI
HEMOS TRANSFORMADO EL PROBLEMA PROPUESTO EN UN PROBLEMA DE CONCURRENCIAS Y ALINEACIONES DE LADOS Y VERTICES DE TRIANGULOS
Estudiemos pues la relación entre los distintos triángulos para poder probar lo que el enunciado pide.
|
|
TEOREMA |
|
La única herramienta que necesitaremos es el
PRIMER TEOREMA DE DESARGUES
Sean ABC y A’B’C’ dos triángulos con vértices y lados distintos. Las intersecciones de los lados tomados dos a dos, es decir los puntos
P = AB ∩ A’B’, Q = BC ∩ B’C’, R = CA ∩ C’A’
están alineados si y sólo si las rectas
AA’, BB’, CC’
son concurrentes.
Una demostración completa se encuentra en el problema 218 de las páginas de RICARDO BARROSO CAMPOS
|
|
DESARROLLO Y SOLUCION |
|
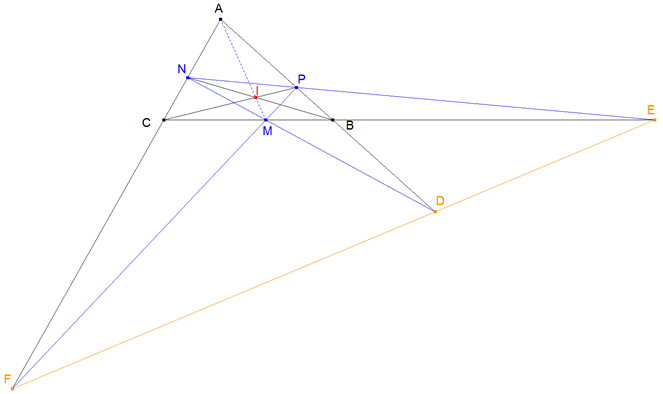
PASO I los triángulos ABC y MNP
Es fácil ver las rectas que unen los vértices de los dos triángulos son concurrentes (Definición y propiedades del punto de Nagel)
Entonces, aplicando el TEOREMA DE DESARGUES podemos afirmar que los puntos de intersección de sus lados están alineados. La recta sobre la que están alineados es EDF.
Resumiendo, los triángulos, aquí vistos, son homológicos y su eje de homología es DE que contiene a F punto de concurrencia de AN y PM.
HASTA AQUI HEMOS DEMOSTRADO LA CONCURRENCIA DE AN, PM y DE.
Vamos ahora a demostrar que la recta ab también concurre en F.
|
|
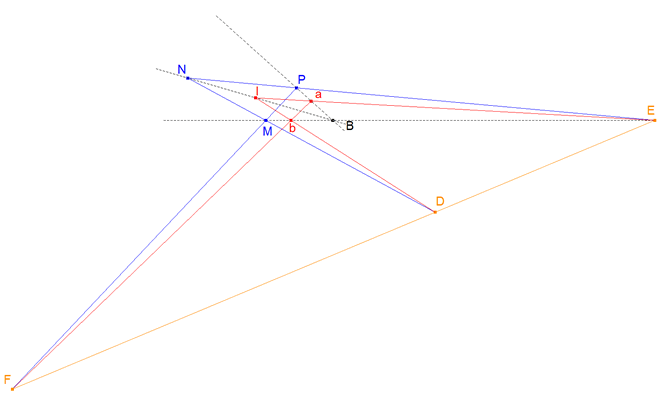
PASO II los triángulos MNP y abI
Sabemos que los lados del triángulo MNP pasan por los puntos D, E y F.
Por construcción dos lados del triángulo abI también pasan por D y E.
Ahora bien, las rectas que unen los vértices de los dos triángulos concurren en B, por lo tanto estos dos triángulos también son homológicos y por lo tanto sus terceros lados también serán concurrentes sobre la recta DE.
Pero MP corta a DE en F, y como ab debe también concurrir con PM en DE entonces ab pasa por F.
Que con el resultado del PASO I nos queda que
AN, PM, DE y ab SON CONCURRENTES
tal como queríamos demostrar.
|