Propuesto por Maite Peña Alcaraz, estudiante de Industriales en
Problema 250.-
625. En un triángulo ABC se toman los puntos
M, N y P de contacto de los círculos exinscritos en
los ángulos A, B y C con los lados BC, CA y AB respectivamente. Se une N con M
y con P, cortando la recta NM a AB en D, y
Siendo a el punto común de IE y AB, y b el de
intersección de ID con BC, demostrar que las rectas AN, PM, DE y ab concurren en un mismo punto
Espeso, G. (1947) MATEMATICA ELEMENTAL Revista publicada por el
instituto Jorge Juan de matemáticas y
Solución de Saturnino Campo Ruiz,
profesor del IES Fray Luis
de León, de Salamanca.-
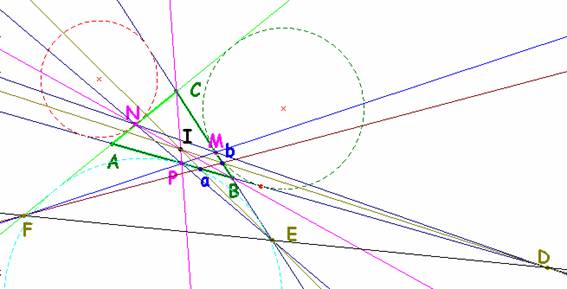
Los puntos M, N y P son los extremos de las cevianas llamadas escisores que dividen al triángulo ABC en dos triángulos de igual perímetro, según se vió en el problema nº 131. Los escisores concurren en un punto, llamado punto de Nagel. Así pues I es el punto de Nagel del triángulo.
Que las rectas AM, BN y CP concurren en el punto de Nagel I, significa que los triángulos ABC y MNP son homológicos en sentido de Desargues, con centro de homología el punto I.
El eje de esta homología es la
recta unión de los puntos de intersección de los pares de lados homólogos: D=ABÇMN
, E=BCÇNP y F=ACÇPM. Con esto queda
probada la concurrencia de tres de las cuatro rectas del enunciado, AN=AC;
PM y DE.
Para la alineación con F de la recta que pasa por los puntos a=IE ÇAB y b=ID ÇBC consideramos la proyección desde este punto F de la recta AB sobre BC.
En esta proyección a la terna (A, P, D ) de la primera le corresponde la terna (C, M, E) en BC. B es un punto doble en esta proyectividad y el eje de la misma o recta de Pappus es la construida con los puntos I=AMÇPC y N=PEÇDM: la recta INB.
Con el eje de la proyectividad es fácil ver que el punto a se proyecta en el punto b=a’. El eje de la proyectividad contiene los puntos de la forma XY’ Ç X’Y, donde X, Y son dos puntos de la primera recta y X’ e Y’ sus homólogos en la segunda.
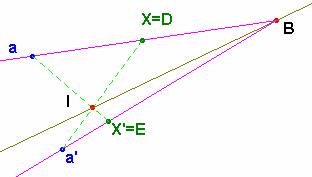
Tomando X=D, su homólogo en la proyección es X’=E. La recta aE corta al eje, recta IB, en el punto I; a’ es la proyección de D sobre BC desde I, es decir, a’ = IDÇBC = b como se quería demostrar.
Obsérvese que en la demostración no se ha utilizado la propiedad específica de los puntos M, N y P de ser los de contacto de los círculos exinscritos. Esto prueba que lo anterior es cierto para cualquier terna M, N , P de puntos que sean pies de cevianas concurrentes.
El papel del punto F no
es singular, puede demostrarse igualmente para el punto E que IFÇAB
e IDÇAC
están alineados con él, y también que IFÇBC e IEÇAC
están alineados con D.