Problema 251

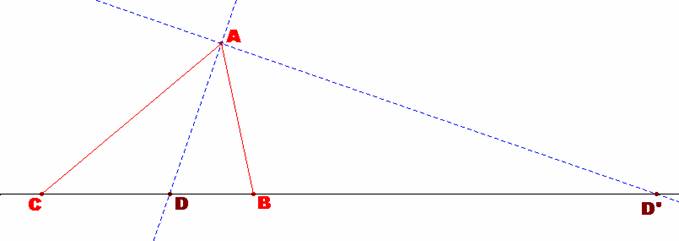
Sea ABC un triángulo. Probar que :

a) Si la bisectriz interior del ángulo A corta a la base en D,
entonces:    AB.AC = AD^2 + BD.DC.
         Enunciar el recíproco y demostrarlo.
¿ Qué ocurre si D es un punto de la base BC de un triángulo isósceles ?

b) Si la bisectriz exterior del ángulo A de un triangulo ABC corta a BC en D´,
entonces: AB.AC = BD´.CD´-AD´^2.
       Hacer las mismas consideraciones de problemas propuestos en a).

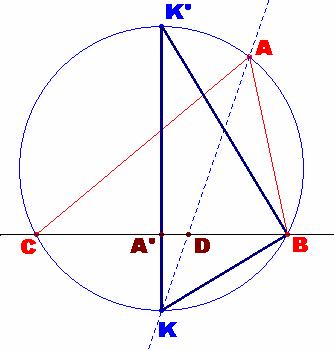
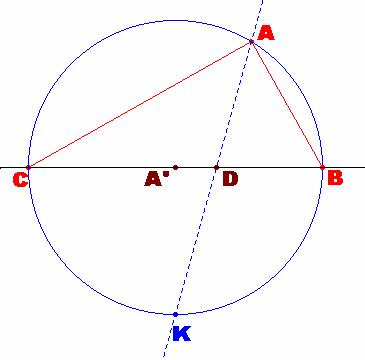
c) Si K es el punto en donde la bisectriz interior del ángulo A corta al círculo circunscrito al triángulo ABC, probar que :
i)  AK. DK = BK^2.
ii) AB. AC = AK^2−BK^2.

d) ABC es un triángulo rectángulo en A intersecando la bisectriz en A a su círculo circunscrito en K.
Probar que  2 AK^2 = (AB+AC)^2.

Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid.

Anjaneyulu,M.S.R (1964). Elements of Modern Pure Geometry, Publishing House, Asia.

Solución de F. Damián Aranda Ballesteros, profesor de Matemáticas del
IES Blas Infante, Córdoba (España).

Sea dado el triángulo ABC, de lados AB = c, AC = b, BC = a; sean asimismo AD y AD’, las bisectrices interior y exterior del ángulo A, respectivamente y los segmentos CD = m, DB = n, CD’=m’ y BD’=n’. Se trata de probar que:
a) AB.AC = AD^2 + BD.DC b^2= AD^2 + m^2 −2∙AD∙m∙cos(B+A/2) c^2= AD^2 + n^2 −2∙AD∙n∙cos(p−(B+A/2) b^2∙n= AD^2∙n + m^2∙n −2∙AD∙m∙n∙cos(B+A/2) c^2∙m= AD^2∙m + n^2∙m +2∙AD∙m∙n∙cos(B+A/2) b^2∙n + c^2∙m = AD^2∙( n + m) + m∙n∙( m + n); Como quiera que, por el teorema de la bisectriz interior tenemos que: ; entonces b∙n = c∙m. Así la anterior expresión la escribimos como: b∙c∙m + c^2∙m = AD^2∙( n + m) + m∙n∙( m + n); c∙m∙(b + c) = (AD^2 + m∙n)∙( n + m); Luego entonces: b∙c = AD^2 + m∙n ; AB.AC = AD^2 + BD.DC En el caso que el triángulo sea isósceles, con los lados iguales b y c, tenemos que, AD sería la altura relativa al vértice A y se verificaría por el teorema de Pitágoras la relación: b^2 = AD^2 + m^2 ; AB^2 = AD^2 + CD^2	b) AB.AC = AD’^2 − BD’.D’C b^2= AD’^2 + m’^2 −2∙AD’∙m’∙cosD’ c^2= AD’^2 + n’^2 −2∙AD’∙ n’∙cos D’ b^2∙n’= AD’^2∙n’ + m’^2∙n’ −2∙AD’∙m’∙n’∙cosD’ c^2∙m’= AD’^2∙m’ + n’^2∙m’ −2∙AD’∙m’∙n’∙cosD’ b^2∙n’ − c^2∙m’ = AD’^2∙( n’−m’) + m’∙n’∙( m’−n’); Como quiera que, por el teorema de la bisectriz exterior tenemos que: ; entonces b∙n’ = c∙m’. Así la anterior expresión la escribimos como: b∙c∙m’ − c^2∙m’ = AD’^2∙( n’−m’) + m’∙n’∙( m’− n’); c∙m’∙(b − c) = (−AD^2 + m∙n)∙( m’−n’); Luego, entonces: b∙c = m’∙n’−AD^2 ; AB.AC = BD.DC − AD^2
Los recíprocos en ambos casos serían válidos al quedar unívocamente determinada la posición de los pies de las bisectrices interior y exterior, D y D’ y al apartado anterior.

c) Si K es el punto en donde la bisectriz interior del ángulo A corta al círculo circunscrito al triángulo ABC, probar que :
i)  AK. DK = BK^2. Como el punto K pertenece a la mediatriz del lado BC, entonces el triángulo KBK’ es rectángulo en B, siendo K’ el punto diametralmente opuesto a K. Por el teorema del cateto, tenemos que: BK^2 = A’K ∙ KK’ (1) Considerando la semejanza entre los triángulos rectángulos KBK’ y KA’D, podemos considerar la relación: y así tenemos que A’K ∙ KK’ = AK ∙ DK Sustituyendo esta última igualdad en (1) resulta: BK^2 = A’K ∙ KK’ = AK ∙ DK	ii) AB. AC = AK^2− BK^2. BK^2= AK^2 + AB^2 −2∙AKAB∙cosA/2 BK^2= AK^2 + AC^2 −2∙AK∙AC∙cosA/2 AC∙BK^2= AC∙AK^2 + AC∙AB^2 −2∙AC∙AK∙AB∙cosA/2 AB∙BK^2= AB∙AK^2 + AB∙AC^2 −2∙AB∙AK∙AC∙cosA/2 (AC−AB)∙BK^2= (AC−AB)∙AK^2 − AC∙AB∙(AC−AB) BK^2= AK^2 − AC ∙ AB Es decir, AB. AC = AK^2− BK^2

d) ABC es un triángulo rectángulo en A. La bisectriz en A corta a su círculo circunscrito en K.
Probar que  2∙AK² = (AB+AC)².

Desarrollando el cuadrado del binomio y teniendo en cuenta el teorema de Pitágoras y el apartado c), obtenemos:
(AB+AC)² = AB² + AC² + 2∙ AB∙ AC = BC² + 2∙ AB∙ AC = BC² + 2∙ (AK² − BK²) = 2∙AK² + BC² −2∙ BK²

Como quiera que BC² = 2∙ BK², entonces se verifica, en efecto, que 2∙AK² = (AB+AC)²