Para el aula
Problema 252
Si ABC es un triángulo equilátero, hallar el lugar geométrico de un
punto D tal que DA = DB + DC
Propuesto por Francisco Javier García Capitán , profesor del IES
Álvarez Cubero (Priego de Córdoba)
Conant L.L. (1905): Original
exercises in plane and solid geometry, American book company,
Solución de F.
Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba, España.
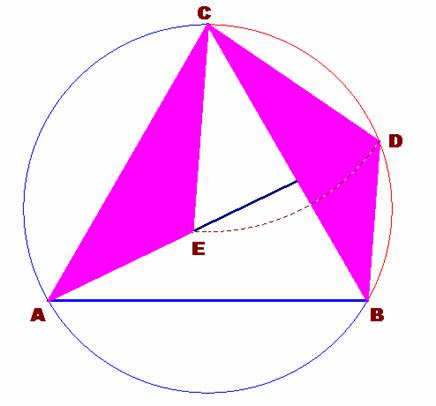
Dado el triángulo equilátero ABC y su circunferencia circunscrita,
situamos el punto D sobre el arco que subtiende como cuerda el lado BC, opuesto
al vértice A.
De esta forma construimos el triángulo equilátero CDE. En efecto este
triángulo es equilátero ya que el ángulo inscrito en D abarca el mismo arco que
el ángulo B del triángulo ABC. Como CD = CE por construcción, entonces el
ángulo en E también es de 60º y así el triángulo CDE es equilátero.
Observamos ahora otro par de triángulos congruentes entre sí. Son AEC y
CDB y aparecen coloreados en la figura dada. Ambos son obtusángulos con un
ángulo igual a 120º, el D y el E, respectivamente. Sus lados opuestos, son
también iguales por ser estos los lados AC y BC del triángulo equilátero ABC.
Además tienen otro par de lados iguales, el CE y CD, por tratarse de lados del
triángulo equilátero CDE. En definitiva, ambos triángulos son congruentes y
así, de este modo AE = DB.
Resumiendo ambos hechos, tenemos que: DA
= DE + EA = DC + DB
Por otra parte, si D es un punto del L.G. solicitado, tenemos que construyendo
el rayo AD, este interceptará a la circunferencia circunscrita en un punto D*,
que pertenecerá usando el razonamiento anterior al L.G. Por la linealidad de la
condición establecida no queda más remedio que D=D*