Para el aula
Problema 252
Propuesto por Francisco Javier García Capitán ,
profesor del IES Álvarez Cubero (Priego de Córdoba)
215. Si ABC es un triángulo equilátero, hallar el lugar geométrico de un
punto D tal que DA = DB + DC
Conant L.L. (1905): Original
exercises in plane and solid geometry, American book company,
Solución del editor.
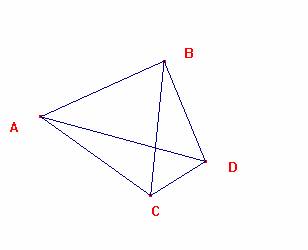
Supongamos que D cumple lo establecido siendo ABC equilátero.
Hagamos un giro con centro en B y amplitud 60, del triángulo BDC.
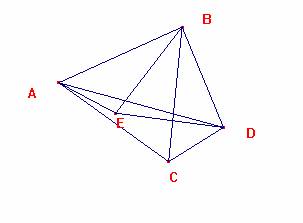
Es CD=AE, BD=BE, y BDE es equilátero, con lo que BD=BE=DE.
Así, es AD=BD+DC, lo que nos lleva a que debe de ser: AD=AE+DE.
Ello significa que el triángulo ADE debe ser “degenerado”.
Al deber estar E sobre AD, el triángulo equilátero construido BDE implica que
El ángulo <BDE=<BDA=60, y al ser <BCA=60, el punto D debe estar sobre la circunferencia circunscrita.
Luego el lg pedido es la circunferencia circunscrita a ABC.
Ricardo Barroso Campos
Didáctica de las Matemáticas
Universidad de Sevilla