Si lo adaptamos al
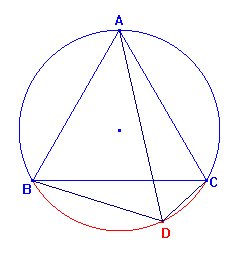
cuadrilátero ABDC, tendremos | Si ABC es un triángulo equilátero, hallar el lugar geométrico de un punto D tal que DA = DB + DC. |
|
Conant L.L. (1905): Original exercises in plane and solid geometry. |
Solución de Francisco Javier García Capitán
Usaremos la desigualdad de Ptolomeo. Según podemos ver en http://garciacapitan.auna.com/escritos/ptolomeo.zip,
Si ABCD es un cuadrilátero cualquiera del plano, entonces AB·CD + BC·DA ³ AC·BD, cumpliéndose la igualdad si y solo si el cuadrilátero es cíclico y convexo.
Si lo adaptamos al
cuadrilátero ABDC, tendremos
Si ABDC es un cuadrilátero cualquiera del plano, entonces AB·DC + BD·CA ³ AD·BC, cumpliéndose la igualdad si y solo si el cuadrilátero es cíclico y convexo.
Pero en la suposición de que el triángulo ABC es equilátero la desigualdad es equivalente a DB + DC ³ DA.
Como conclusión, para que se cumpla la igualdad la condición necesaria y suficiente es que D esté en el arco BC que no contiene a A de la circunferencia circunscrita a ABC.