Teorema de
Ptolomeu.
Un
quadrilàter ABCD és cíclic (inscrit en una circumferència) si i només si la
suma dels productes dels costats oposats és igual al producte de les diagonals 
.
Problema 252
Proposat per Francisco
Javier García Capitán ,
professor de l’IES Álvarez Cubero
(Priego de Córdoba)
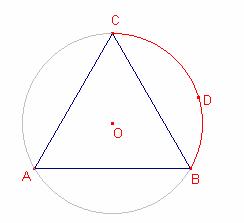
Siga el triangle equilàter 
. Determineu el lloc geomètric d’un punt D tal que
Conant L.L. (1905): Original
exercises in plane and solid geometry, American book company,
Solució:
Siga D un punt en l’arc menor 
de la circumferència
circumscrita al triangle .
Provem
que
Siga 
el costat del triangle equilàter .
El
quadrilàter ADBC es inscrit en la circumferència circumscrita del triangle .
Aplicant
el teorema de Ptolomeu:
Per
ser el triangle equilàter:
Simplificant:
.
Al
contrari si , aleshores, A, B, C, D formen un quadrilàter cíclic i D
pertany al menor arc .