Teorema de Ptolomeo.

Un cuadrilátero ABCD es cíclico (inscrito en una circunferencia) si i sólo si la suma de los productos de los lados opuestos es igual al producto de las diagonales .

Problema 252

Propuesto por Francisco Javier García Capitán , profesor del IES Álvarez Cubero (Priego de Córdoba)

215. Si es un triángulo equilátero, hallar el lugar geométrico de un punto D tal que DA = DB + DC

Conant L.L. (1905): Original exercises in plane and solid geometry, American book company, New York (p. 35)

York (p. 35)

Solución:

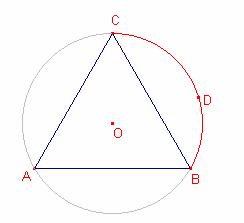
Sea D un punto en el arco menor de la circunferencia circunscrita al triángulo .

Probemos que

Sea el lado del triángulo equilátero .

El cuadrilátero ADBC está inscrito en la circunferencia circunscrita del triángulo .

Aplicando el teorema de Ptolomeo:

Por ser el triángulo equilátero:

Simplificando:

.

Al contrario si , entonces, A, B, C, D forman un cuadrilátero cíclico y D pertenece al menor arco .