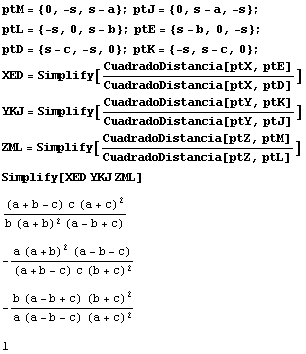
|
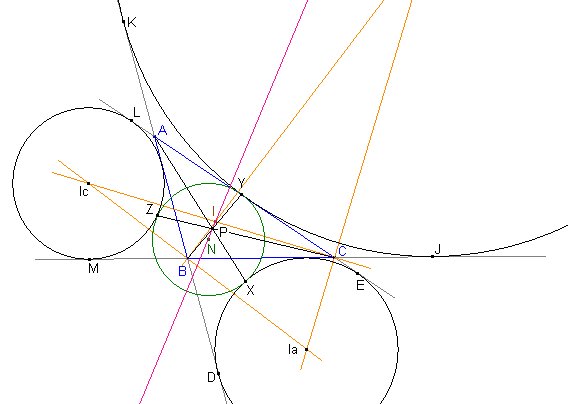
Los excírculos (Ia), (Ib), (Ic) determinan con el círculo de los nueve puntos (centro N, radio r) del triángulo ABC los puntos de tangencia X, Y, Z respectivamente. Además (D, E),(K, J),(M, L) son los puntos de tangencia sobre (AB, AC), (BA, BC), (CB, CA) con los excírculos (Ia), (Ib), (Ic) respectivamente. Probar que:
|
|
Propuesto por Juan Carlos Salazar |
Solución de Francisco Javier García Capitán.
Comenzamos por trazar la figura, incluyendo las circunferencias y los puntos de tangencia que cita el enunciado:

Usaremos Mathematica y las coordenadas baricéntricas
![]()
|
El notebook Baricentricas.nb contiene las instrucciones que usaremos aquí y otras más para trabajar con coordenadas baricéntricas. Una buena idea es colocarlo en alguno de los directorios accesibles a Mathematica, por ejemplo, C:\Archivos de programa\Wolfram Research\Mathematica\5.1\AddOns\ExtraPackages Estos directorios dependen de la instalación realizada. Para obtener una lista de los directorios accesibles a Mathematica, podemos teclear $Path. Aquí puedes ver una versión en pdf de Baricentricas.nb |
Para hallar los puntos X, Y, Z, que están definidos como intersecciones de circunferencias tangentes, usaremos que estos puntos dividen al segmento que une los centros en una razón conocida: la resultante de dividir los radios de las dos circunferencias.
Si el radio de la circunferencia circunscrita a ABC es R, sabemos que el radio de la circunferencia de los nueve puntos es exactamente la mitad, (1/2)R.
Llamando ra al radio de la circunferencia exinscrita con centro Ia, y D al área del triángulo ABC tenemos las relaciones:
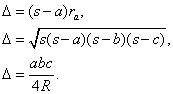
A partir de ellas calculamos:
![]()
Introducimos directamente las coordenadas del excentro Ia:
![]()
Hallamos las coordenadas del centro N de la circunferencia de los nueve puntos teniendo en cuenta que N es el punto medio del circuncentro y el ortocentro.
![]()
![]()
Ahora podemos hallar el punto X, pues conocemos los extremos
del segmento NIa y la razón con la que X divide
a dicho segmento:
![]()
De forma análoga hallamos las coordenadas de los puntos
Y y Z.
![]()
![]()
![]()
![]()
Ahora comprobamos que las rectas AX, BY y CZ son concurrentes:

![]()
Para hallar las coordenadas del punto P hallamos la intersección de dos de las tres rectas:
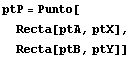
![]()
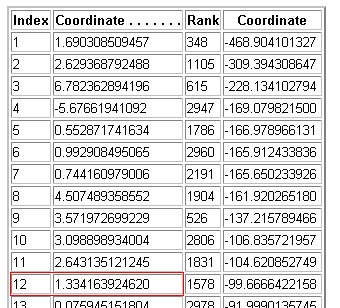
¿Será un punto conocido? Para buscarlo en la Enciclopedia de Clark Kimberling introducimos
![]()
![]()
Al buscar la coordenada obtenida encontramos que P es el punto X(12), descrito como el conjugado armónico del punto de Feuerbach respecto del incentro y el centro de la circunferencia de los nueve puntos.
El punto de Feuerbach (F en la figura siguente) es el punto de contacto de la circunferencia de los nueve puntos y la circunferencia inscrita al triángulo. Ambas circunferencias son tangentes en virtud del teorema de Feuerbach.
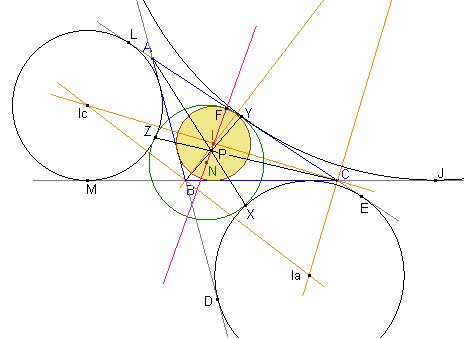
Para empezar por lo más fácil, podemos calcular la perspectriz de los triángulos ABC y XYZ, es decir, la recta en la que se alinearán las intersecciones de AB y XY, BC y YZ, CA y ZX.

![]()
Es decir, la ecuación de la perspectriz es bc x + ca y + ab z = 0.
Veamos que esta es también la recta de Monge de los tres excírculos. Para ello calculamos, por ejemplo el punto X1 de intersección de la recta IbIc con la recta BC, que será el punto de corte de las dos tangentes exteriores a las circunferencias (Ib) e (Ic).
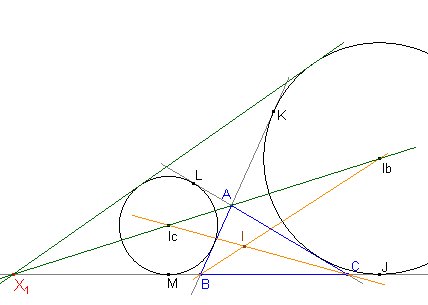
Entonces hacemos
![]()
Y análogamente

Es evidente que estos tres puntos pertenecen a la recta bc x + ca y + ab z = 0.
La primera parte es sencilla:
![]()
![]()
Para comprobar la segunda, calculamos
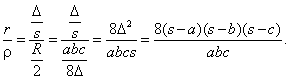
Y ahora, usando Mathematica,
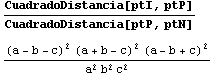
Aquí, a falta de un método más elegante, usamos la fuerza bruta de Mathematica:
Las coordenadas de los puntos de tangencia de los excírculos con los lados del triángulo se obtienen fácilmente. Por ejemplo, sabemos que BM:MC = -(s-a):a, y ánálogamente para los otros. Entonces: