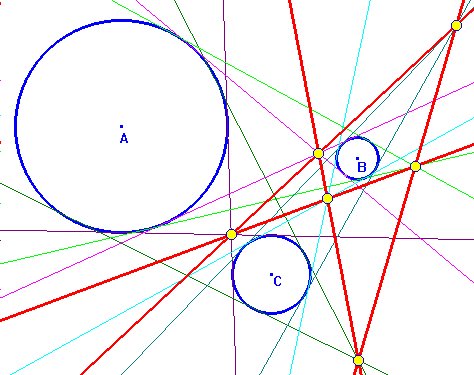
|
Los excírculos (Ia), (Ib), (Ic) determinan con el círculo de los nueve puntos (centro N, radio r) del triángulo ABC los puntos de tangencia X, Y, Z respectivamente. Además (D, E),(K, J),(M, L) son los puntos de tangencia sobre (AB, AC), (BA, BC), (CB, CA) con los excírculos (Ia), (Ib), (Ic) respectivamente. Probar que:
|
|
Propuesto por Juan Carlos Salazar |
Solución de Francisco
Javier García Capitán
|
Dadas tres circunferencias se cumplen:
|
Como consecuencia, los seis centros de semejanza están alineados tres a tres en cuatro rectas:
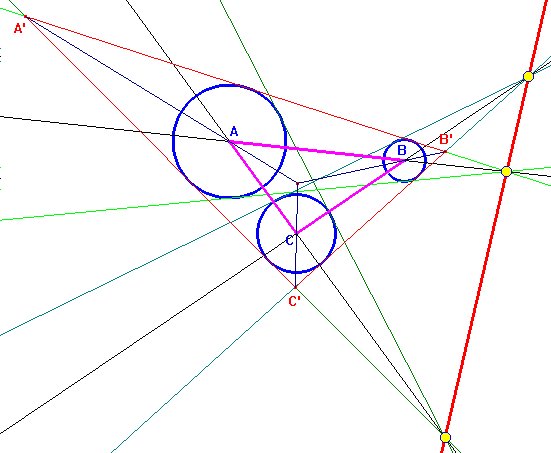
La demostración para el caso de los tres centros de semejanza directos usando el teorema de Desargues que reproducimos aquí está tomada de la web de Alexander Bogomolny. Considerando el triángulo A'B'C' formado por las tangentes exteriores, resulta que AA', BB' y CC' son sus bisectrices interiores, por lo que se cortarán en un punto, el incentro de A'B'C'. Por tanto, según el teorema de Desargues, los puntos de intersección de AB y A'B', BC y B'C', y CA y C'A' estarán alineados.
La demostración original de Monge usa el espacio tridimensional. (Puede encontrarse en el §32. "The Tangency Problem of Apollonius", en H. Dörrie: 100 Great Problems of Elementary Mathematics, their history and solution) y la reproducimos aquí:
|
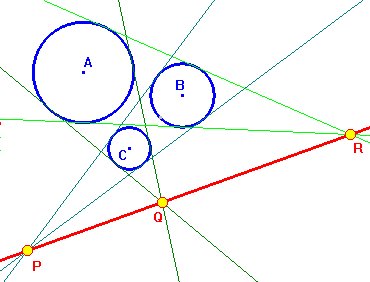
Sean P, Q, R los centros de homotecia de las circunferencias (B,C), (C, A) y (A, B). Al girar el par de circunferencias (B, C) alrededor del eje PBC obtenemos las esferas B, C y su cono tangente con vértice en P. Algo parecido ocurre con los otros pares de circunferencias. Ahora consideremos dos planos E y F tangentes a las tres esferas, todas ellas quedando por el mismo lado de cada plano (podemos imaginar que las esferas están sobre el plano de una mesa y que ponemos un folio de papel sobre ellas). Como los tres conos serán tangentes a las a los planos, estos contendrán a los vértices y por tanto los tres vértices P, Q, R estarán en la recta de intersección de los dos planos. |
 |
|
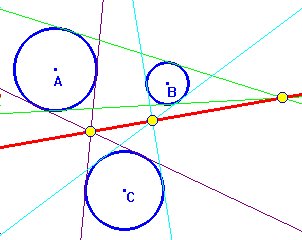
Para demostrar el caso de los centros de homotecia inversos de los pares (A, C) y (B, C) y el centro de homotecia directo del par (A, B) consideramos los planos E y F de manera que las esferas A y B quedan en un lado de cada plano y la esfera C queda en el otro. |
 |
El siguiente razonamiento puede encontrarse en el mensaje número 6135 (de Darij Grinberg) en el grupo de noticias Hyacinthos (para ver los mensajes de este grupo hay que registrarse)
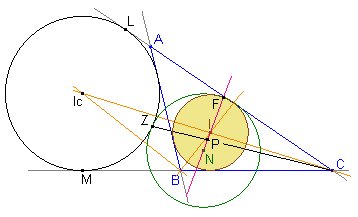En
la figura de la derecha tenemos un triángulo ABC, y las circunferencias
inscrita, de los nueve puntos y exinscrita correspondiente al vértice
C.
Hemos destacado los puntos de contacto F y Z de la circunferencia de los nueve puntos con la circunferencia inscrita y con la circunferencia exinscrita correspondiente al vértice C, respectivamente.
El punto F, llamado punto de Feuerbach, es el centro de semejanza directo de dichas circunferencias. Su conjugado armónico P respecto de los centros N e I será el centro de semejanza inverso.
Por tanto, tenemos:
Según el teorema de las tres circunferencias de Monge, P, Z y C están alineados. Como lo mismo ocurre con P, X, A y P, Y, B, queda demostrado que
|
AX, BY, CZ son concurrentes en
P.
|
Lo que sigue es de mi cosecha:
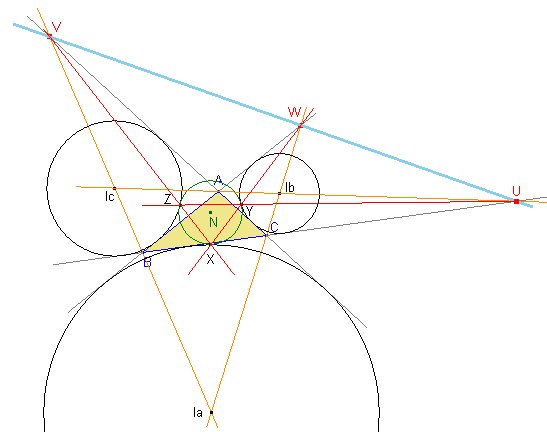Ahora,
en la figura de la derecha tenemos las circunferencias exinscritas y sus centros
de homotecia directos U, V y W, que están alineados en
virtud del teorema de las tres circunferencias de Monge. La recta que pasa por
los tres puntos es la recta de Monge.
Pero si consideramos las circunferencias (Ia), (Ic), y la circunferencia de los nueve puntos tenemos que V es el centro de semejanza directo de (Ia) e (Ic), X es el centro de semejanza inverso de (Ia) y la circunferencia de los nueve puntos, y Z es el centro de semejanza inverso de (Ic) y la circunferencia de los nueve puntos. Por tanto X, Z y V están alineados. Esto indica que ZX e IcIa se cortan en V.
Análogamente, W es la intersección de XY e IaIb, y U es la intersección de YZ e IbIc.
Todo esto permite afirmar que
|
La perspectriz de los triángulos ABC y XYZ
es la recta de Monge de los tres excírculos,
|
ya que cada recta está determinada por tres puntos alineados que resultan ser los mismos.
Por ser P el centro de semejanza inverso de la circunferencia inscrita (con centro I y radio r) y la circunferencia de los nueve puntos (con centro N y radio r), es evidente que
|
P es colineal con N e I. Además
se cumple: IP : PN = r : r.
|
Queda pendiente la demostración de la igualadad
|
XE ·YK
·ZM = XD ·YJ ·ZL
|
y esta solución queda incompleta en este punto.