Problema 254

Construir un triángulo dados un lado a, el radio R de la circunferencia circunscrita y la distancia e entre el punto de intersección de sus alturas y el centro de dicha circunferencia.

MATEMATICA ELEMENTAL (1948) Revista publicada por el instituto Jorge Juan de matemáticas y la Real Sociedad Matemática Española 4ª Serie – Tomo VIII nº5 EJERCICIOS RESUELTOS

Propuesto por Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid).

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba, España.

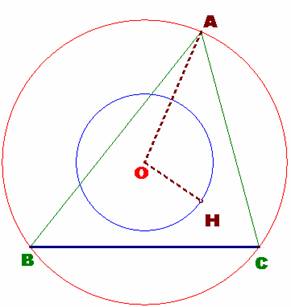
Dado el triángulo ABC y su circunferencia circunscrita de centro O, situamos en la figura los datos que se nos dan. Sean pues dados el lado BC, el radio OA y la distancia OH.

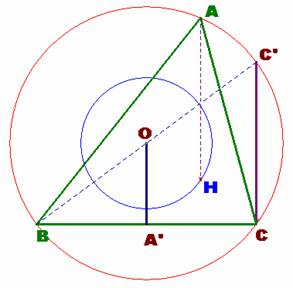Analizando el triángulo ya construido observamos que podemos construir sin dificultad la circunferencia de centro O y radio OA así como la cuerda BC. Trazamos la circunferencia de centro O y radio OH y ya todo quedará pendiente de la localización del punto H ya que, a partir de éste punto, podremos cerrar la figura ABC sin ninguna dificultad.


Sabemos que , donde C' es el punto diametralmente opuesto al punto B y A' es el punto medio del lado BC. Así que la circunferencia trasladada según el vector cortará a la circunferencia de centro O y radio OH en el punto H, ortocentro del triángulo ABC.