Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid
Problema 254
Construir un triángulo dados un lado a, el radio R de la circunferencia circunscrita y la distancia e entre el punto de intersección de sus alturas y el centro de dicha circunferencia.
Matemática Elemental(1946) 4 Serie, Tomo VI, Madrid, problemas propuestos, Números, 7-8, página 275
Solución del director
Dado el lado a y el radio de la circunscrita, podemos construir el circuncentro O.
El ortocentro H estará sobre la circunferencia Ω de centro O y radio e.
El simétrico de H según a está sobre la circunscrita, por lo que el punto de corte de la simétrica de Ω respecto al lado a, será el simétrico de H, por lo que podemos obtener H. Así el problema tendrá dos, una o ninguna solución.
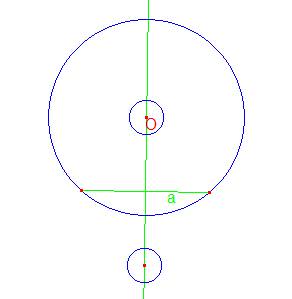
Caso sin solución. La simétrica de Ω respecto al lado a no tiene puntos de corte con la circunscrita.
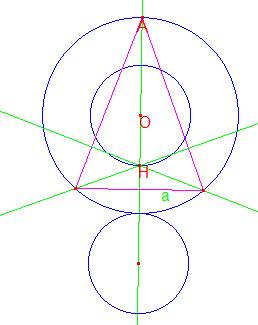
Caso de solución única: La simétrica de Ω respecto al lado a es tangente con la circunscrita.
El triángulo es isósceles.
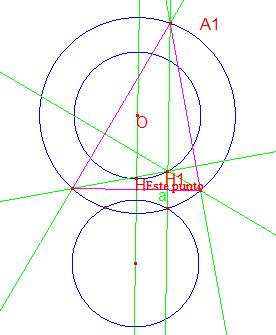
Caso de dos puntos de corte entre la simétrica de Ω respecto al lado a y la circunscrita.
Habría dos triángulos.
Realmente siguiendo estrictamente el enunciado, no ha lugar al primer caso.
Se plantea este caso al considerar todas las posibilidades.
Ricardo Barroso Campos.
Didáctica de las Matemáticas.
Universidad de Sevilla.