Propuesto por Juan Bosco Romero Márquez, profesor
colaborador de
Problema 596
Construir un triángulo dados un lado a, el radio R de la circunferencia circunscrita y la distancia e entre el punto de intersección de sus alturas y el centro de dicha circunferencia.
Matemática Elemental(1946) 4 Serie, Tomo VI, Madrid, problemas propuestos, Números, 7-8, página 275
Nota del director: El profesor Ángel Montesdeoca informa que este problema ya ha sido publicado en esta revista con el número 254, en Junio de 2005.De esta manera, se sustituirá por otro 254 el 1 de diciembre. El director agradece la atención.
Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES
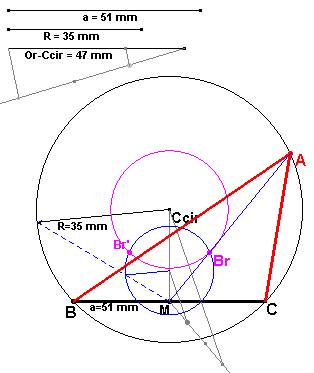 El triángulo
se resuelve hallando el baricentro Br mediante la intersección de dos lugares
geométricos.
El triángulo
se resuelve hallando el baricentro Br mediante la intersección de dos lugares
geométricos.
El baricentro Br está en la mediana AM del lado a, a una distancia de
su pie M de AM/3. En consecuencia, el
lugar geométrico de los posibles baricentros Br formarán una circunferencia homotética
a la circunscrita, de razón 1/3 cuyo centro de
homotecia es el punto M.
El baricentro Br también está en el segmento de Euler cuyos extremos
son el punto de intersección de sus alturas (ortocentro Or) y el centro de la
circunferencia circunscrita Ccir, o sea, el dato dado. La distancia del
baricentro Br al circuncentro Ccir es 1/3 del segmento de Euler. En
consecuencia, el lugar geométrico de los posibles baricentros Br formarán una
circunferencia de radio 1/3 del segmento de Euler cuyo centro es el circuncentro
Ccir.