Propuesto por Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid). Problema 254 598. Construir un triángulo dados un lado a, el radio R de la circunferencia circunscrita y la distancia e entre el punto de intersección de sus alturas y el centro de dicha circunferencia. MATEMATICA ELEMENTAL (1948) Revista publicada por el instituto Jorge Juan de matemáticas y la Real Sociedad Matemática Española 4ª Serie – Tomo VIII nº5 EJERCICIOS RESUELTOS Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de junio de 2005) |
|
¿DÓNDE ESTÁ EL CIRCUNCENTRO DEL TRIÁNGULO? |
|
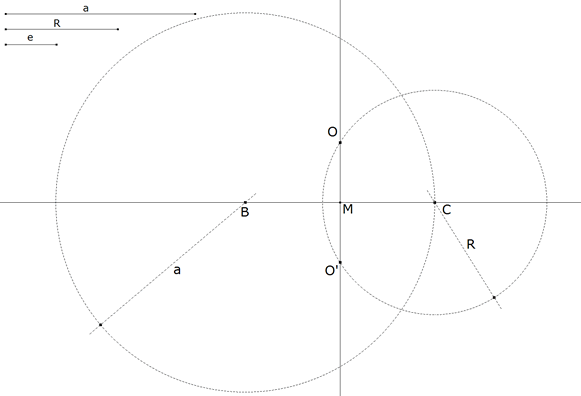
El circuncentro O, es el punto de intersección de las mediatrices del triángulo. Como tenemos el lado BC=a podemos determinar su mediatriz MO como perpendicular a BC por M punto medio de BC. O está sobre la mediatriz MO. Además O equidista de B y C, que a su vez pertenecen al círculo circunscrito, una distancia R. O está sobre el círculo Γ de centro C ( o B ) y radio R.
figura 1 Tomamos en el plano un punto B. Con centro en B, círculo de radio a; tomamos C sobre el círculo. Por M, punto medio de BC trazamos la perpendicular a BC (mediatriz). Con centro en C, círculo Γ de radio R (radio del círculo circunscrito). Este último círculo Γ corta a la mediatriz en O y O’. Tomamos O como circuncentro de nuestro triángulo. ¡Ojo, O’ también nos será útil!
|
|
¿DÓNDE ESTÁ EL ORTOCENTRO DEL TRIÁNGULO? |
|
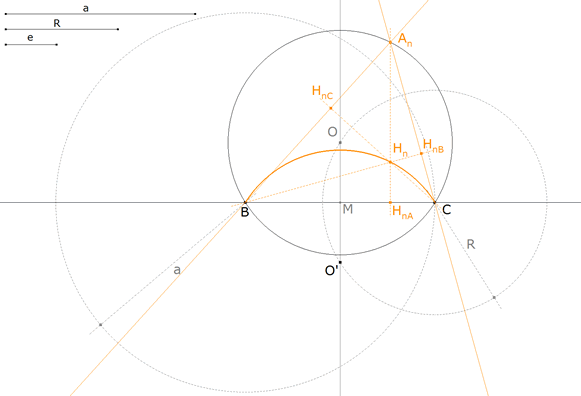
Sabemos que el vértice A está sobre el círculo circunscrito. Supongamos que tenemos el problema resuelto y trazamos un vértice cualquiera An. Trazamos las alturas correspondientes y obtenemos el ortocentro Hn y los pies de las alturas HnA, HnB y HnC. Estudiamos el ángulo BHnC.
figura 2 El triángulo AnHnBHn y el triángulo AnHnAC son semejantes; los dos tienen un ángulo recto y comparten un mismo ángulo. Entonces el tercer ángulo también coincide y
Del mismo modo, comparando los triángulos rectángulos AnHnCHn y AnHnB
Y de aquí
Este ángulo es constante, entonces el ortocentro está sobre un arco de círculo de base BC y arco capaz π-A. El arco superior del círculo circunscrito con base la cuerda BC es el arco capaz del ángulo A, suplementario de π-A. Deducimos que el ortocentro está sobre el círculo simétrico del círculo circunscrito respecto al eje BC. Este círculo no es más que el círculo ΓO’ de centro O’ que pasa por B y C. El enunciado dice que el ortocentro se encuentra a una distancia e de O; está en el círculo Γe de centro O y radio e.
|
|
SOLUCIÓN |
|
DETERMINACIÓN DE EL ORTOCENTRO
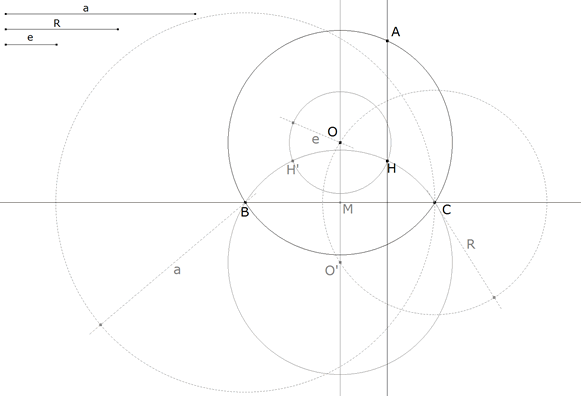
figura 3 Con centro en O’ trazamos la circunferencia que pasa por B y C. Con centro en O trazamos la circunferencia de radio e. Las circunferencias se cortan en H y H’. Desarrollamos la solución con H.
|
|
DETERMINACIÓN DEL VÉRTICE A La altura por el vértice A pasa por H. A está en HA la perpendicular por H a BC. A está también sobre el círculo circunscrito ΓABC.
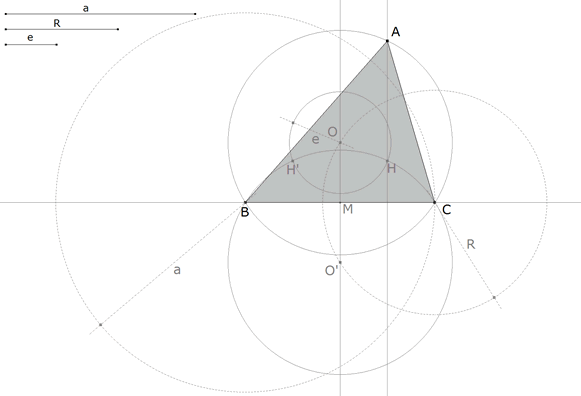
figura 4 Perpendicular por H a BC. Circunferencia de centro O que pasa por B y C. La intersección de la perpendicular y la circunferencia, en la parte superior de la cuerda BC (ángulo A) determina el vértice A.
|
|
ABC EL TRIÁNGULO BUSCADO
figura 5
|