Problema 254

Propuesto por Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid).

598. Construir un triángulo dados un lado a, el radio R de la circunferencia circunscrita y la distancia e entre el punto de intersección de sus alturas y el centro de dicha circunferencia.

MATEMATICA ELEMENTAL (1948) Revista publicada por el instituto Jorge Juan de matemáticas y la Real Sociedad Matemática Española 4ª Serie – Tomo VIII nº5 EJERCICIOS RESUELTOS

Solución:

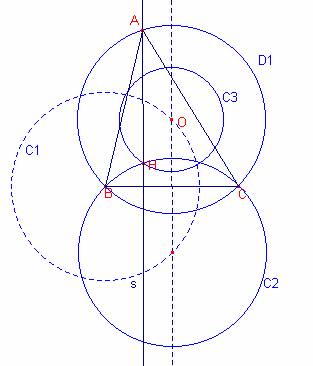
a) Dibujar el segmento .

b) Dibujar la mediatriz del segmento .

c) Dibujar la circunferencia C1 de centro B y radio R.

d) La intersección de la mediatriz y la circunferencia C1 da el circuncentro O del triángulo .

e) Dibujar la circunferencia D1 de centro O que pasa por B (circunferencia circunscrita al triángulo).

f) Dibujar la circunferencia C2 simétrica de la circunferencia C1 respecto del segmento (arco capaz de ).

g) Dibujar la circunferencia C3 de centro O y radio e.

h) Dibujar la intersección de les circunferencias C2 C3 que da el ortocentro H.

i) Dibujar la recta s perpendicular al segmento que pasa por H.

j) La intersección de s i la circunferencia C1 da el vértice A.

Con Cabri:

Figura barroso254b.fig

Applet created on 16/06/05 by Ricard Peiró with CabriJava