| Construir un triángulo conociendo, en posición, sus tres bisectrices y un punto sobre el perímetro del triángulo. |
|
Juan Sapiña Borja: Problemas gráficos de Geometría. Propueso por Jose María Pedret |
Solución de Francisco Javier García Capitán
Análisis:
 |
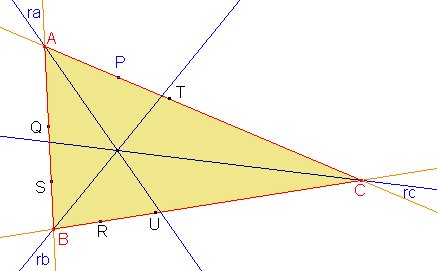
Supongamos el problema resuelto como en la figura, en el que el punto dado P pertenece al lado AC del triángulo buscado ABC.
Los puntos simétricos Q y R del punto P respecto de las bisectrices de los ángulos A y C deberán estar en los lados AB y CB, respectivamente.
A su vez, los simétricos de los puntos obtenidos respecto de las rectas correspondientes estarán en otros lados del triángulo.
Construcción:
Dadas las rectas ra, rb y rc y el punto P, como en la figura, hallamos los puntos Q y R simétricos de P respecto de ra y rc, respectivamente. A continuación, hallamos los puntos S, simétrico de R respecto de rb, y T, simétrico de S respecto de ra. Finalmente, U es el simétrico de T respecto de rc (o también el simétrico de Q respecto de rb).
Así tendremos dos puntos en cada lado del triángulo buscado, y el triángulo podrá obtenerse trazando las rectas PT, QS y RU.
Observaciones:
| Observemos que, llamando I al punto de intersección de las tres rectas dadas, las distancias de I a P, Q, R, S, T, U serán todas iguales. Por ejemplo, al ser Q el simétrico de P respecto de la recta ra, el tirángulo IPQ será isósceles y tendremos IP=IQ. |
|
|
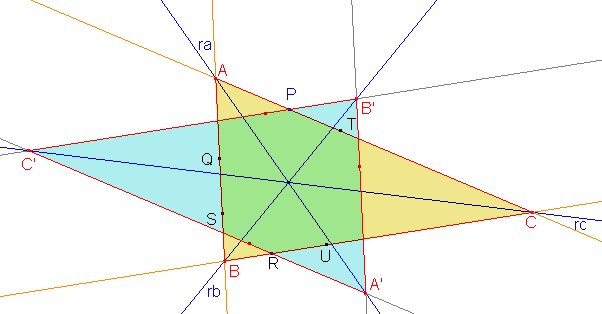
| En el caso especial que P=T, Q=S y R=U, sucederá que P, Q y R son los puntos de contacto de la circunferencia inscrita con los tres lados, y también podremos hallar el triángulo ABC trazando la circunferencia con centro I y radio P y la recta tangente a la misma por el punto P, que determinará con dos de las rectas dadas dos de los vértices del triángulo buscado. |
|
Finalmente, obtendremos otra solución si repetimos lo mismo, pero suponiendo que P es un punto del lado BC.
 |