Problema 255

Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona

411 Construir un triángulo conociendo, en posición, sus tres bisectrices y un punto sobre el perímetro del triángulo.

Sapiña, J. (1955): Problemas Gráficos de Geometría,Litograf. Madrid.

(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solución:

Supongamos el problema resuelto.

Sea el triángulo que tiene incentro I. Sean las tres rectas (1, 2, 3) bisectrices.

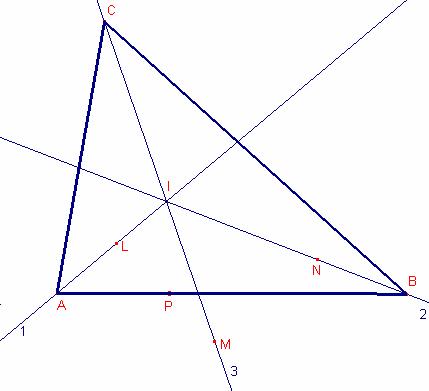
Sea x el ángulo que forman las rectas 1 y 3, .

Sea y el ángulo que forman las rectas 2 y 3, .

Siga , .

Entonces, ,

Por tanto, , .

Dibujamos un triángulo cualquiera con los ángulos anteriores.

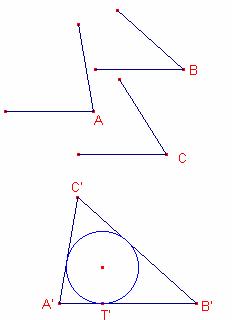
Después he construido un triángulo igual al anterior que tenga el incentro I y las mismas bisectrices que el que buscamos.

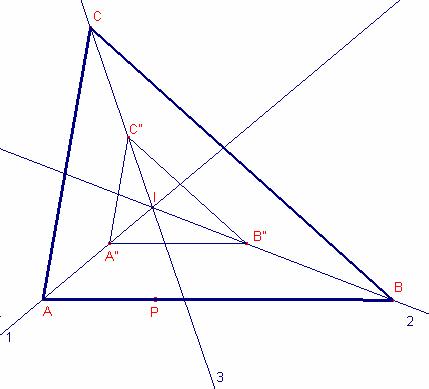
He dibujado la recta paralela al lado que pasa por P.

He determinado A y B.

He dibujado la recta paralela al lado que pasa por A.

He determinado C.

He dibujado el triángulo .

Solución con CABRI:

Figura barroso255.fig

Applet created on 16/06/05 by Ricard Peiró with CabriJava