Problema 255

Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona

411 Construir un triángulo conociendo, en posición, sus tres bisectrices y un punto sobre el perímetro del triángulo.

Sapiña, J. (1955): Problemas Gráficos de Geometría,Litograf. Madrid.

(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solución 2:

Supongamos el problema resuelto.

Sea el triángulo que tiene incentro I. Sean las tres rectas (1, 2, 3) bisectrices.

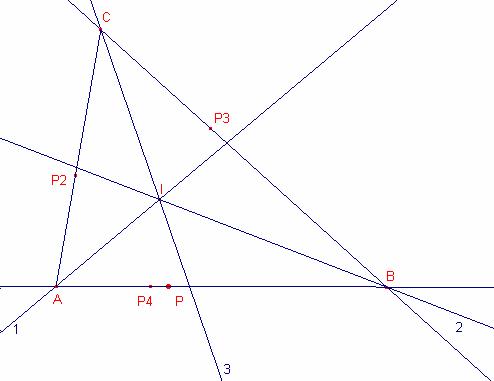
a) Sea P2 el simétrico de P respecto de la recta1. Este punto pertenece al lado b (o prolongación del lado b)

b) Sea P3 el simétrico de P2 respecto de la recta3. Este punto pertenece al lado a (o prolongación del lado a).

c) Sea P4 el simétrico de P3 respecto de la recta2. Este punto pertenece al lado b (o prolongación del lado b)

d) Sea la recta que pasa por los puntos P P4 que corta las rectas 1 y 2 en los puntos A, B respectivamente:

e) La recta que pasa por los puntos A, P2 corta la recta 3 en el punto C.

f) Dibujamos el triángulo

Solución con CABRI:

Figura barroso255b.fig

Applet created on 19/06/05 by Ricard Peiró with CabriJava