Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona

Problema 256

Este problema fue propuesto y resuelto por APOLONIO en su obra "De Sectione Spatii". La obra se perdió, pero HALLEY la restableció a partir de una traducción árabe.

Julius Petersen. Méthodes et théories pour la résolution des problèmes de constructions géométriques. Gauthier-Villars. Paris (1880); PROBLÈME 366.

Juan Sapiña Borja. Problemas gráficos de Geometría. Litograf. Madrid 1955. Capítulo de áreas, PROBLEMA 637.

Enunciado
Por un punto dado P, trazar una recta que forme con otras dos rectas dadas, un triángulo de área dada.

Sea A el punto de intersección de las rectas dadas; se representa el área dada bajo la forma de un triángulo, del que un lado es AP y el otro está sobre una de las rectas dadas. La recta buscada debe ser tal que el elemento de área que se añade al triángulo sea igual al que determina la sección en el triángulo. Pero esas dos áreas son triángulos cuyas alturas son conocidas. La razón de las bases de esos triángulos es pues conocida también y en consecuencia, el problema se transforma en el enunciado auxiliar que sigue.

Enunciado, también de APOLONIO en su obra "De Sectione Rationis", obra perdida y restablecida en parte por HALLEY.

Julius Petersen. Méthodes et théories pour la résolution des problèmes de constructions géométriques. Gauthier-Villars. Paris (1880); PROBLÈME 363.

Enunciado auxiliar
Se dan dos rectas, sobre cada una de ellas un punto, A y B, y un punto exterior P. Trazar por P una recta que encuentra a las rectas dadas en X e Y de tal manera que los segmentos AX y BY estén en una razón dada.

El 4 de julio se añade esta indicación, que Petersen incluye en el problema

Se determina el centro de rotación O de las rectas dadas, considerando A

y B, al igual que X e Y, como puntos homólogos. La razón dada es la razón de

semejanza. Como entonces OXY es semejante a OAB la recta OP será vista desde

X bajo un ángulo conocido en consecuencia X se determina fácilmente

POR UN PUNTO DADO P, TRAZAR UNA RECTA QUE FORME CON OTRAS DOS RECTAS DADAS UN TRIÁNGULO DE ÁREA DADA

Solución del profesor Nicolás Rosillo, Dpto. Matemáticas, IES Máximo Laguna (Santa Cruz de Mudela, Ciudad Real)

Sin pérdida de generalidad la situación dada se describe mediante una configuración como la siguiente: las rectas dadas contienen a los puntos (a,b),(a,0) y (a,b),(c,0) y la recta a obtener contiene a (0,0)

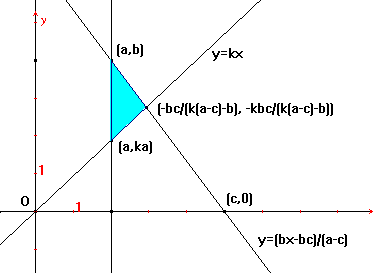
Resolviendo que el área del triángulo sea igual a z, se obtienen cuatro soluciones de k en función de a, b, c y z; de ellas sólo dos son válidas según los valores de a, b y c.