PROBLEMA 256 |
| Solución de José María Pedret Yebra. Ingeniero Naval. Esplugues de Llobregat (Barcelona) 1 de julio de 2005 |
Este problema fue propuesto y resuelto por APOLONIO en su obra "De Sectione Spatii". La obra se perdió, pero HALLEY la restableció a partir de una traducción árabe. Julius Petersen. Méthodes et théories pour la résolution des problèmes de constructions géométriques. Gauthier-Villars. Paris (1880); PROBLÈME 366. Juan Sapiña Borja. Problemas gráficos de Geometría. Litograf. Madrid 1955. Capítulo de áreas, PROBLEMA 637. Enunciado Por un punto dado P, trazar una recta que forme con otras dos rectas dadas, un triángulo de área dada. Sea A el punto de intersección de las rectas dadas; se representa el área dada bajo la forma de un triángulo, del que un lado es AP y el otro está sobre una de las rectas dadas. La recta buscada debe ser tal que el elemento de área que se añade al triángulo sea igual al que determina la sección en el triángulo. Pero esas dos áreas son triángulos cuyas alturas son conocidas. La razón de las bases de esos triángulos es pues conocida también y en consecuencia, el problema se transforma en el enunciado auxiliar que sigue. Enunciado, también de APOLONIO en su obra "De Sectione Rationis", obra perdida y restablecida en parte por HALLEY. Julius Petersen. Méthodes et théories pour la résolution des problèmes de constructions géométriques. Gauthier-Villars. Paris (1880); PROBLÈME 363. Enunciado auxiliar Se dan dos rectas, sobre cada una de ellas un punto, A y B, y un punto exterior P. Trazar por P una recta que encuentra a las rectas dadas en X e Y de tal manera que los segmentos AX y BY estén en una razón dada. Se determina el centro de rotación O de las rectas dadas, considerando A y B, al igual que X e Y, como puntos homólogos. La razón dada es la razón de semejanza. Como entonces OXY es semejante a OAB la recta OP será vista desde X bajo un ángulo conocido en consecuencia X se determina fácilmente. |
0. SEMEJANZA - FUNDAMENTOS TEORICOS |
Damos a continuación en NUEVE pasos una serie de ideas sobre la semejanza directa en el plano, que nos ayudan a establecer el método de solución perfilado en el enunciado de Julius Petersen. |
ROTACION Dado un punto O, y un ángulo orientado θ, la transformación del plano que transforma un punto M en un punto M’ tal que recibe el nombre de rotación de centro O y ángulo θ. HOMOTECIA Dado un punto O, y una razón algebraica k, la transformación del plano que transforma un punto M en otro M’ tal que recibe el nombre de homotecia de centro O y razón k. SEMEJANZA Dado un punto O, un ángulo orientado θ y una razón algebraica k, la transformación del plano que transforma un punto M en un punto M’ tal que recibe el nombre de semejanza de centro O, ángulo θ y razón k. |
0.1 Si desde un punto dado O se trazan rectas por los puntos de una curva dada Γ y si se hacen girar esas rectas un ángulo θ al rededor de O, y al mismo tiempo se las hace crecer (o disminuir) según una razón dada k, se obtiene una nueva curva Γ' como lugar geométrico de los extremos de las rectas que así se han hecho girar. 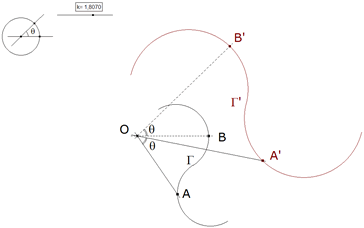 figura 1 Esta nueva curva debe ser semejante a Γ, pues podemos imaginar realizadas las dos operaciones del modo siguiente: En primer lugar, rotación de la curva primitiva (sólo cambia la posición). En segundo lugar, homotecia de razón k respecto a O. Un punto A de la curva Γ determinará por semejanza un punto A' de la curva Γ'. Tales puntos se denominan homólogos. Rectas homólogas son las que unen puntos homólogos, y ángulos homólogos son los formados por rectas homólogas. El punto O puede llamarse centro de semejanza (centro de rotación), θ ángulo de rotación y k la razón de semejanza. Para dos puntos homólogos cualesquiera, A' y A, el triángulo A'OA debe conservar la misma forma ya que AOA'=θ y OA'/OA=k son constantes. Entonces también podemos decir que la curva Γ' es la que describe el vértice A' de un triángulo A'OA que, todo y conservando su forma, gira en torno de su otro vértice O, mientras que el tercer vértice recorre la curva dada. Cuando se trate de expresar que se hace girar una curva en torno a O, un ángulo de rotación θ y razón k, se podrá decir que se transforma la curva por una semejanza de centro O, razón k y ángulo θ. |
0.2 Todo punto del plano puede ser considerado como perteneciente a uno de los dos sistemas (original y transformado); y en consecuencia tendrá su homólogo en el otro. Considerado el centro de rotación desde este punto de vista, será su propio homólogo (punto que se corresponde a sí mismo) y a causa de ello podemos denominarlo también el punto doble de la transformación. Igualmente se puede imaginar que todo el plano gira en torno a O de tal manera que uno de sus puntos recorre une curva dada. Si el sistema completo de puntos del plano conserva su forma durante el movimiento, uno cualquiera de sus puntos describirá una curva semejante a la curva dada. |
0.3 En el momento en que se conoce el centro de rotación, el ángulo y la razón, se puede hacer girar un sistema cualquiera compuesto de rectas y arcos de círculo empleando solamente regla y compás. Se hará girar un punto A alrededor de O tomando AOA’ igual al ángulo de rotación y haciendo OA’=kOA. 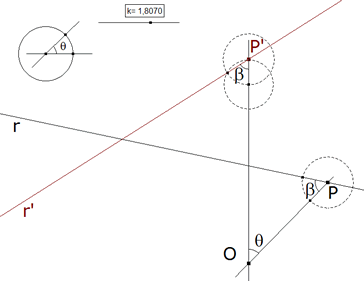 figura 2 Para una recta, sólo habrá que hacer girar uno de sus puntos y trazar la recta que hará con el radio del punto nuevo un ángulo igual al que hacía la recta original con el radio del punto que se hace girar. También se pueden encontrar los homólogos de dos puntos de la recta. 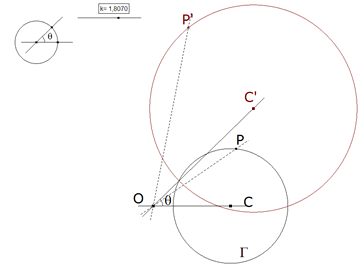 figura 3 Para un círculo, bastará encontrar los homólogos de su centro y de un punto de su circunferencia. |
|
0.5 Dadas dos figuras semejantes; si sus elementos se siguen en el mismo sentido, tendrán siempre un centro de rotación, es decir un punto alrededor del cual se podrá hacer girar una de ellas para que vaya a coincidir sobre la otra; la razón de semejanza está determinada, ya que dos rectas homólogas cualesquiera están según esa razón, y el ángulo de rotación es el ángulo comprendido entre dos rectas homólogas. 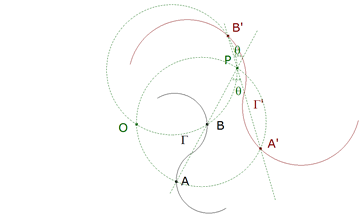 figura 4 Para encontrar el centro de rotación, podríamos utilizar la razón conocida de sus distancias a un par de puntos homólogos y el arco capaz de ángulo θ para dos puntos homólogos; pero puede emplearse una construcción más simple. Sean A y A’, B y B’ dos pares de puntos homólogos. Las rectas homólogas AB y A’B’ deben comprender al ángulo de rotación; este mismo ángulo es también el que harán los radios que unen dos puntos homólogos al centro de rotación; este último debe encontrarse sobre el mismo círculo que el punto de intersección de dos rectas homólogas y de dos puntos homólogos situados sobre estas rectas. El centro de rotación de dos rectas homólogas, en dos figuras semejantes, es el centro de rotación de las propias figuras; pues si se hace girar* una recta de manera que coincida con la otra, una de las figuras deberá también coincidir con la otra. El centro de rotación de dos rectas que se extienden hasta el infinito, consideradas como figuras semejantes, está completamente indeterminado; si sobre las rectas se eligen dos puntos como homólogos, se tiene un círculo como lugar geométrico de los centros de rotación; si se dan otros dos puntos homólogos más o, lo que es lo mismo, la razón de semejanza, el centro de rotación estará completamente determinado; y es único, ya que los círculos se cortan en un segundo punto, el de intersección de las rectas. 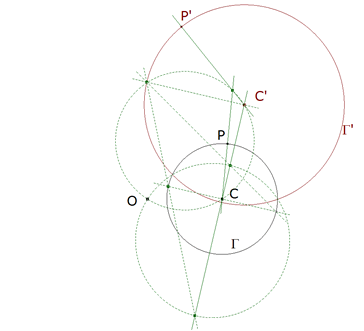 figura 5 Para dos círculos, el centro de rotación es indeterminado, ya que dos cualesquiera de sus puntos pueden considerarse como puntos homólogos; como las distancias del centro de rotación a los centros de los círculos deben estar entre ellas como los radios, el lugar geométrico de este centro será un círculo que divide armónicamente la recta de centros siguiendo esa razón (es el círculo que pasa por los centros de semejanza de los dos círculos dados y tiene sus centro sobre la recta de centros). Si se eligen dos puntos de los círculos como puntos homólogos, el centro de rotación está determinado y se encuentra de la manera más simple con la ayuda de radios homólogos, ya que los centros son siempre puntos homólogos. |
0.6 El centro de rotación de dos lados opuestos de un cuadrilátero es también el centro de rotación de los otros dos. 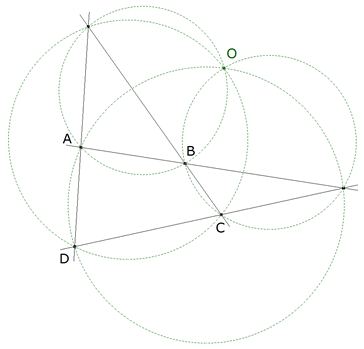 figura 6 Sea O el centro de rotación de BA y CD; entonces AOB es semejante a DOC; pero se deduce fácilmente que AOD es semejante a BOC, y resulta además que O es el centro de rotación de AD y BC. En el primer caso B y C, A y D son puntos homólogos; en el segundo lo son B y A, C y D. Del mismo modo se ve que el centro de rotación de AB y CD es también el de AC y BD. Prolongamos los lados opuestos hasta que se encuentren; los círculos que determinan el centro de rotación están circunscritos a los cuatro triángulos formados en la figura; se deben utilizar los mismos círculos para determinar el centro de rotación de dos elementos cualesquiera de la figura que no se corten en uno de sus extremos; se tiene así el siguiente teorema: ...En un cuadrilátero completo, los círculos circunscritos a los triángulos que se forman, no considerando sucesivamente uno de los lados, pasan por el mismo punto, y este punto es el centro de rotación de dos segmentos cualesquiera de la figura que no se corten en uno de sus extremos... |
0.7 Si se dividen según la misma razón las rectas que unen los puntos homólogos de curvas semejantes, el lugar geométrico de los puntos de división será una curva semejante a las curvas dadas, y dos cualesquiera de esas curvas tienen el mismo centro de rotación que las primeras. 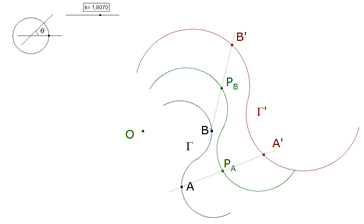 figura 7 Sean A’ y A dos puntos homólogos y supongamos la recta A’A dividida por el punto P según una razón dada. Sea O el centro de rotación; la forma del triángulo A’OA debe permanecer constante; y lo mismo para AOP y en consecuencia P debe describir una curva semejante a las curvas dadas, cuando el triángulo gira alrededor de O. Corolario: Si en un cuadrilátero se trazan dos sistemas de líneas que dividen los dos pares de lados opuestos en partes proporcionales, las líneas de un mismo sistema se dividirán según la misma razón. |
0.8 Si tenemos tres sistemas semejantes A, B y C y si un punto O es el centro de rotación de A y B, al mismo tiempo de B y C, debe ser también el centro de rotación de A y C. Este punto es pues el centro común de rotación de los tres sistemas; y naturalmente lo puede ser también para un número cualquiera de sistemas. 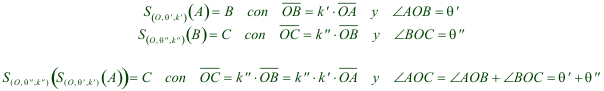 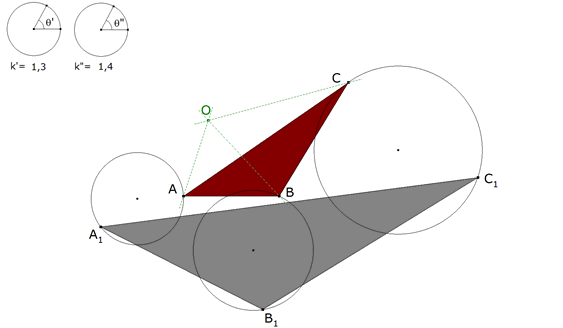 figura 8 Si unimos tres puntos homólogos A, B y C de los tres sistemas con centro de rotación en O, las razones de estas rectas y los ángulos que hacen entre ellas son constantes; resulta que la forma del triángulo ABC es también constante y, por ello, lo denominaremos el triángulo fundamental. Del mismo modo, vemos que a varias figuras semejantes, que tienen un centro común de rotación, corresponde un polígono fundamental de forma constante. Si gira alrededor del centro de rotación de manera que un vértice describe une de las figuras, los otros vértices describirán las otras figuras y cualquier otro punto del plano, considerado como perteneciente al polígono fundamental, trazará una figura semejante a las otras. Como el polígono fundamental llega a tomar sucesivamente todas sus posiciones, el centro de rotación de las figuras dadas es también el centro de rotación del polígono fundamental en todas sus posiciones. |
0.9 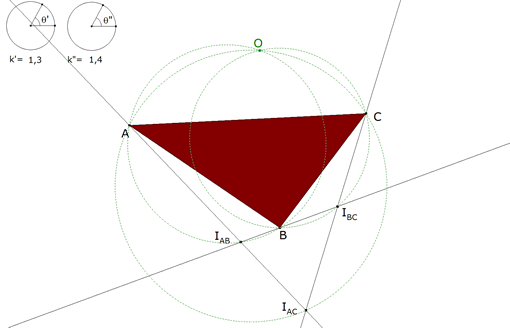 figura 9 Para dos rectas, sobre las que se dan dos puntos como puntos homólogos, el centro de rotación debe encontrarse sobre un círculo que pasa por los dos puntos y el punto de intersección de las rectas dadas; para tres rectas, sobre las que se dan tres puntos como puntos homólogos, el centro de rotación está entonces determinado; es el punto de intersección de dos círculos del mismo tipo; El tercer círculo debe pasar por el mismo punto. Uniendo los tres puntos, se forma el triángulo fundamental; puede pues tener una forma cualquiera ya que se pueden elegir arbitrariamente los tres puntos; pero a los distintos triángulos fundamentales les corresponde distintos centros de rotación. Se puede determinar fácilmente el centro de rotación para un triángulo fundamental dado construyendo sobre las tres rectas un triángulo semejante al triángulo dado y determinando de esta manera tres puntos homólogos. Si las tres rectas pasan por un mismo punto O, este último será el centro de rotación para cada triángulo fundamental, de manera que los triángulos semejantes a un triángulo fundamental dado son semejantes y tienen a O por centro de semejanza. Hay no obstante un caso particular donde el centro de rotación está indeterminado; en efecto, si los vértices A y B del triángulo recorren AO y BO y si ∠C=∠AOB, C recorrerá una recta que pasa por O. |
1. RESOLUCION |
1.1 EL PROBLEMA AUXILIAR |
Se dan dos rectas, sobre cada una de ellas sendos puntos, A y B, y además un punto exterior P. Trazar por P una recta que encuentre a las rectas dadas en X e Y de tal manera que los segmentos AX y BY estén según una razón dada. Se determina el centro de rotación O de las rectas dadas, considerando A y B, al igual que X e Y, como puntos homólogos. La razón dada es la razón de semejanza. Como entonces OXY es semejante a OAB la recta OP será vista desde X bajo un ángulo conocido; en consecuencia X se determina fácilmente. |
1.1.1 DATOS DEL ENUNCIADO  figura 10 dibujamos el enunciado. |
1.1.2 PRIMERA SUGERENCIA DEL ENUNCIADO 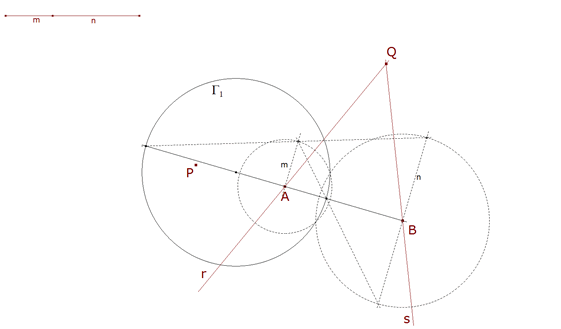 figura 11 Según la indicación del enunciado: “...Se determina el centro de rotación O de las rectas dadas, considerando A y B, al igual que X e Y, como puntos homólogos. La razón dada es la razón de semejanza...” Según 0.5 (figura 5): “...Para dos círculos, el centro de rotación es indeterminado, ya que dos cualesquiera de sus puntos pueden considerarse como puntos homólogos; como las distancias del centro de rotación a los centros de los círculos deben estar entre ellas como los radios, el lugar geométrico de este centro será un círculo que divide armónicamente la recta de centros siguiendo esa razón (es el círculo que pasa por los centros de semejanza de los dos círculos dados y tiene sus centro sobre la recta de centros)...” Obtenemos el círculo Γ1 como primer lugar que contiene al centro de rotación. |
1.1.3 SEGUNDA SUGERENCIA DEL ENUNCIADO 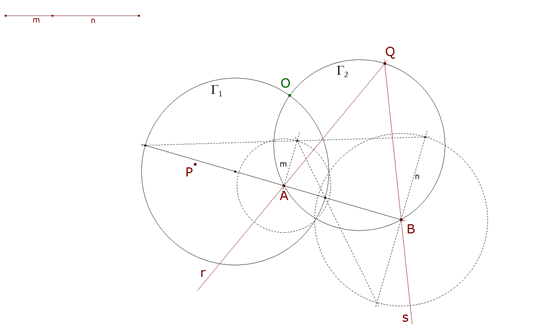 figura 12 Según la indicación del enunciado: “...Se determina el centro de rotación O de las rectas dadas, considerando A y B, al igual que X e Y, como puntos homólogos...” Según 0.5 (figura 4) “...pero puede emplearse una construcción más simple. Sean A y A’, B y B’ dos pares de puntos homólogos. Las rectas homólogas AB y A’B’ deben comprender al ángulo de rotación; este mismo ángulo es también el que harán los radios que unen dos puntos homólogos al centro de rotación; este último debe encontrarse sobre el mismo círculo que el punto de intersección de dos rectas homólogas y de dos puntos homólogos situados sobre estas rectas...” Tomando A y B como homólogos y Q punto de intersección de las rectas dadas, obtenemos el círculo Γ2 como segundo lugar que contiene al centro de rotación. |
1.1.4 TERCERA SUGERENCIA DEL ENUNCIADO 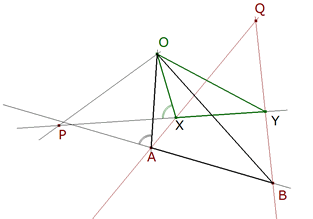 figura 13 Según la indicación del enunciado: “...Como entonces OXY es semejante a OAB la recta OP será vista desde X bajo un ángulo conocido en consecuencia X se determina fácilmente...” En la figura 13 vemos la causa. Si suponemos el problema resuelto deducimos el ángulo bajo el que se ve OP desde X |
1.1.5 EL ARCO CAPAZ QUE CONTIENE A X 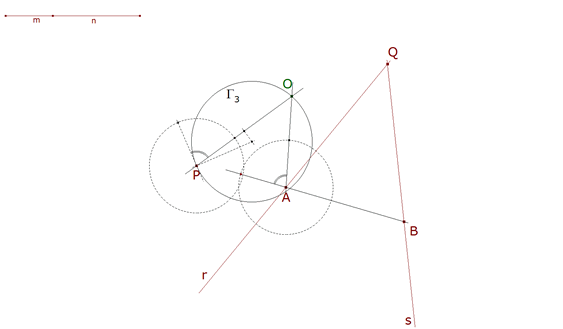 figura 14 Determinamos entonces π-∠OAB y lo trasladamos como arco capaz de OP. Como desde X se ve OP bajo ese ángulo, X está sobre el círculo Γ3 que acabamos de dibujar con el arco capaz mencionado. |
1.1.6 DETERMINACION DE X 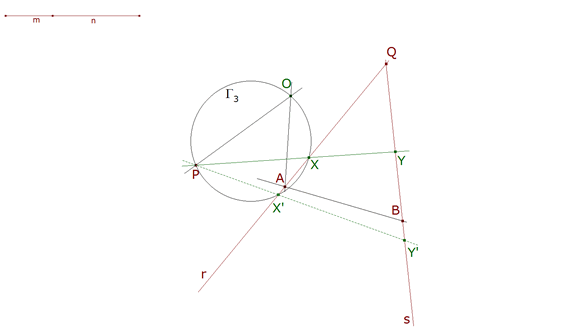 figura 15 Pero X además está sobre la recta r=AQ, entonces y a lo sumo puede haber dos soluciones pues un círculo corta a la recta en cero, uno o dos puntos. 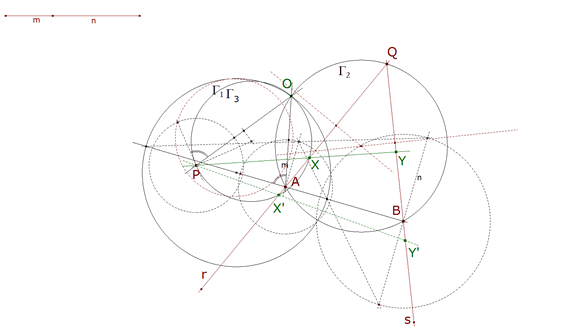 figura 16 Así queda con todas las líneas vistas. |
1.2 EL PROBLEMA PRINCIPAL |
Por un punto dado P, trazar una recta que forme con otras dos rectas dadas, un triángulo de área dada. Sea A el punto de intersección de las rectas dadas; se representa el área dada bajo la forma de un triángulo, del que un lado es AP y el otro está sobre una de las rectas dadas. La recta buscada debe ser tal que el elemento de área que se añade al triángulo sea igual al que determina la sección en el triángulo. Pero esas dos áreas son triángulos cuyas alturas son conocidas. La razón de las bases de esos triángulos es pues conocida también y en consecuencia, el problema se transforma en el problema auxiliar anterior. |
1.2.1 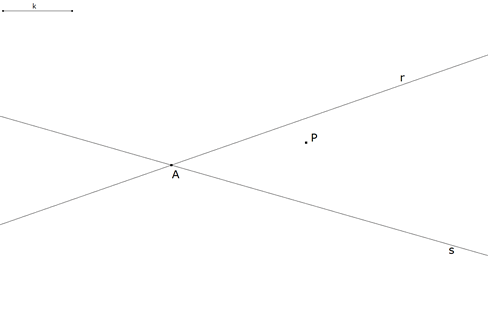 figura 17 Dibujamos el enunciado. |
1.2.2 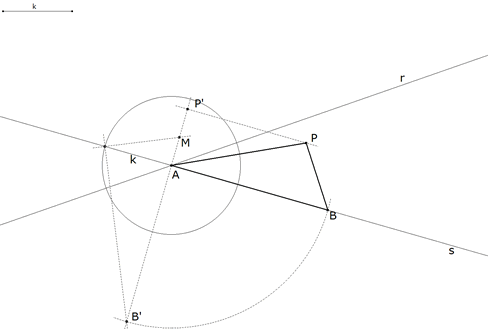 figura 18 Según la indicación del enunciado: “... Sea A el punto de intersección de las rectas dadas; se representa el área dada bajo la forma de un triángulo, del que un lado es AP y el otro está sobre una de las rectas dadas ...” Es decir dado un segmento k hallar B sobre s tal que Sea M el punto medio de P’A. Por P una paralela a s y por A una perpendicular a s determinan P’. La perpendicular a la recta, que une M con la intersección de s y el círculo de centro A y radio k, corta a P’A en B’. AB’ es la base del triángulo buscado y PS su altura. Llevamos AB’ sobre s y determinamos B. |
1.2.3 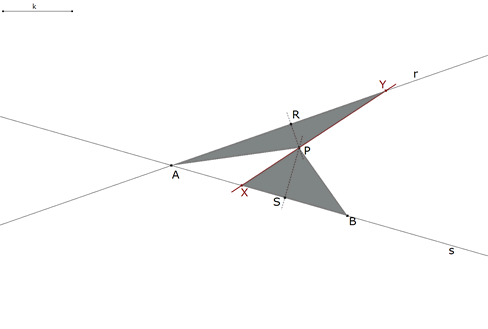 figura 19 Según la indicación del enunciado: “... La recta buscada debe ser tal que el elemento de área que se añade al triángulo sea igual al que determina la sección en el triángulo. Pero esas dos áreas son triángulos cuyas alturas son conocidas. La razón de las bases de esos triángulos es pues conocida también y en consecuencia, el problema se transforma en el problema auxiliar ...” Supongamos para ello que tenemos el problema resuelto, entonces En la última relación es fácil ver el problema auxiliar donde la razón dada es la razón de las distancias del punto P a las rectas dadas. Sigamos pues con el procedimiento desarrollado en el problema auxiliar. |
1.2.4  figura 20 Para determinar el centro de giro, como hemos visto en 1.1.2 (figura 11), trazamos el círculo de Apolonio para los puntos B y A con razón de distancias Tenemos el círculo Γ1 como primer lugar geométrico que contiene al centro de giro. |
1.2.5 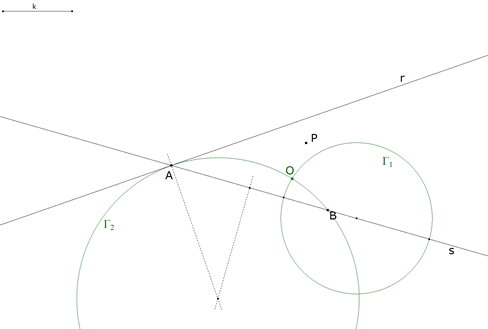 figura 21 Como hemos visto en 1.1.3 (figura 12), trazamos el círculo que pasa por los puntos B, A y la intersección de las rectas dadas; pero A es ese punto, entonces como B y A son puntos de s, considerando A también como punto de r, resulta que el círculo será tangente a r en A. La mediatriz de BA y una perpendicular a r en A determinan el centro del círculo buscado. Tenemos el círculo Γ2 como segundo lugar geométrico que contiene al centro de giro |
1.2.6 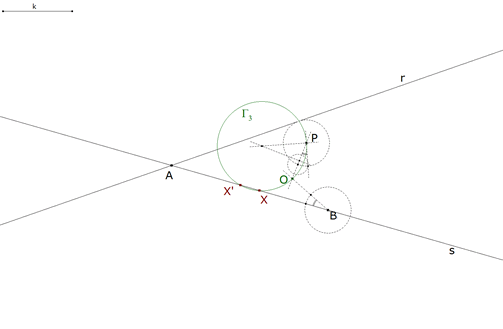 figura 22 Como hemos visto en 1.1.5 (figura 16), determinamos el ángulo OBA. Trazamos ahora el arco capaz del ángulo OBA y segmento OP. Tenemos el círculo Γ3 como lugar geométrico de los puntos X que se ven desde OP bajo un ángulo OBA. Pero X además está sobre la recta s=AB, entonces |
1.2.7 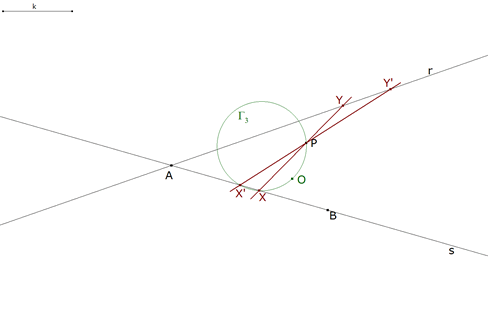 figura 23 La recta XP que corta a la recta s en Y y la recta X’P que corta a s en Y’ son las soluciones pedidas. |
1.3 LA SOLUCION DE JUAN SAPIÑA BORJA |
Exponemos ahora una solución completamente distinta que Juan Sapiña, su autor, denomina método de isogonales. La solución de su libro no contempla los pasos constructivos intermedios (figuras 25, 26, 27). CEVIANAS ISOGONALES Dos rectas que parten del vértice de un ángulo se llaman isogonales, respecto a los lados del mismo; cuando forman con ellos ángulos iguales, es decir; cuando son simétricas respecto a la bisectriz del ángulo considerado. |
1.3.1 PLANTEO  figura 24 Supuesto el problema resuelto, trazamos PA que forma un ángulo α con AY. Trazamos la recta que forma un ángulo α con AX y corta al círculo circunscrito AXY en E. Entonces los triángulos YAP y XEA son semejantes por la igualdad de los ángulos γ Que es una propiedad de las isogonales. Como conocemos el ángulo A y el área podemos escribir todos son valores conocidos y además (figura 24) |
1.3.2 CONSTRUCCION 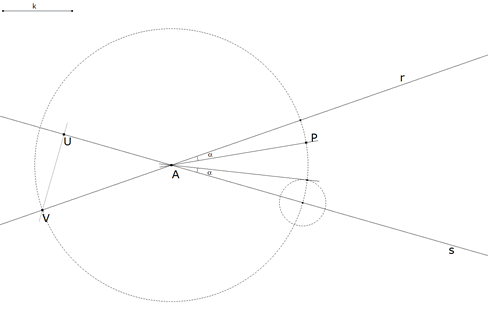 figura 25 Llevamos el ángulo α desde A sobre la recta s; además |
1.3.3 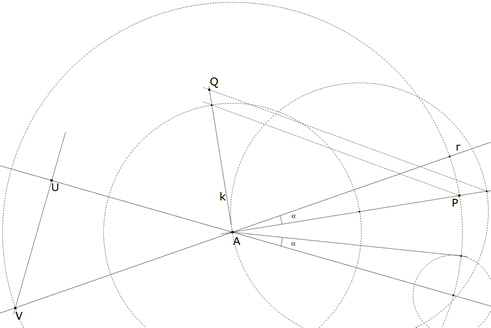 figura 26 Trazamos ahora AQ que nos permite trazar AE 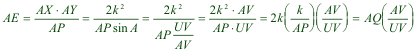 Basta dibujar (ver figura 26) |
1.3.4 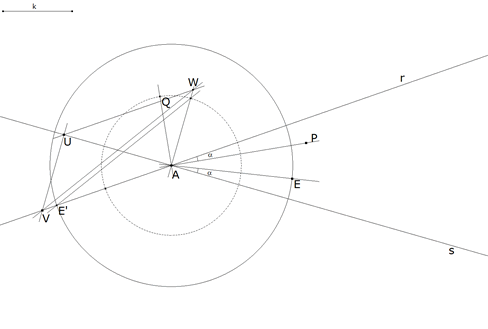 figura 27 Acabamos de trazar AE haciendo Por A paralela a UV y por U paralela a AV determinan W tal que UV=AW paralela a VW por la intersección de AW y del círculo de radio AQ; esta paralela corta a AV en E’ tal que AE’=AE. |
1.3.5 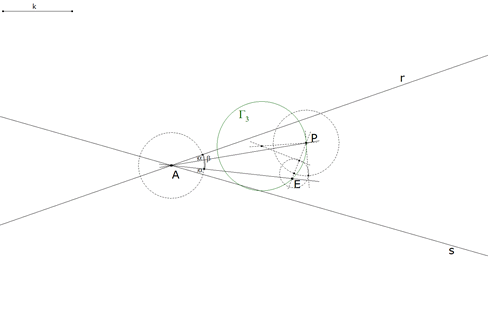 figura 28 Sobre PE trazamos el arco capaz de ángulo Obtenemos el círculo Γ3 lugar geométrico de los puntos X desde los que se ve PE bajo un ángulo β. ¡Es el mismo círculo Γ3 hallado en 1.2.5 (figuras 22 y 23) |
1.3.6 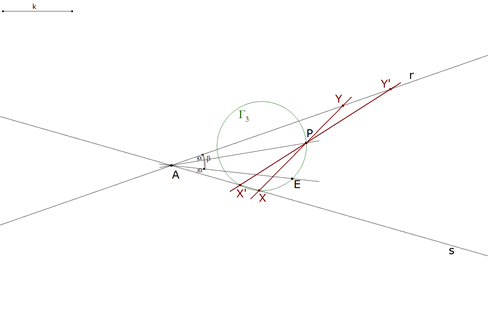 figura 29 Pero X además está sobre la recta s, entonces La recta XP que corta a la recta s en Y y la recta X’P que corta a s en Y’ son las soluciones pedidas. |