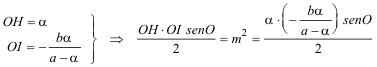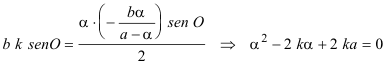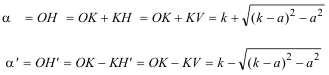“...Este problema fue propuesto y resuelto por APOLONIO en su obra "De Sectione Spatii". La obra se perdió, pero HALLEY la restableció a partir de una traducción árabe.

Julius Petersen. Méthodes et théories pour la résolution des problèmes de constructions géométriques. Gauthier-Villars. Paris (1880); PROBLÈME 366.

Juan Sapiña Borja. Problemas gráficos de Geometría. Litograf. Madrid 1955. Capítulo de áreas, PROBLEMA 637...”

Así es como empezaba el enunciado que propuse en su día.

 

Georges Ritt. Problèmes d’application de algèbre à la géométrie avec les solutions développées. Librairie de L. Hachette. Paris 1857.

Generalmente, hacemos un planteamiento geométrico, la complementamos con alguna manipulación algebraica y concluimos la construcción geométrica que resuelve el problema.

El atractivo es, en este caso, que de un planteamiento puramente algebraico deducimos el método geométrico.

Otro añadido del atractivo de esta solución es que la construcción desarrollada es completamente distinta a las otras dos soluciones presentadas, en su día; y distinta también de la solución analítica presentada por Nicolás Rosillo.

Para la solución tomamos las rectas dadas como ejes de coordenadas; por tanto trabajamos en ejes oblicuos.

 

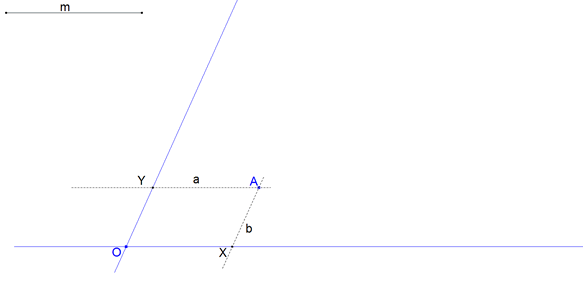
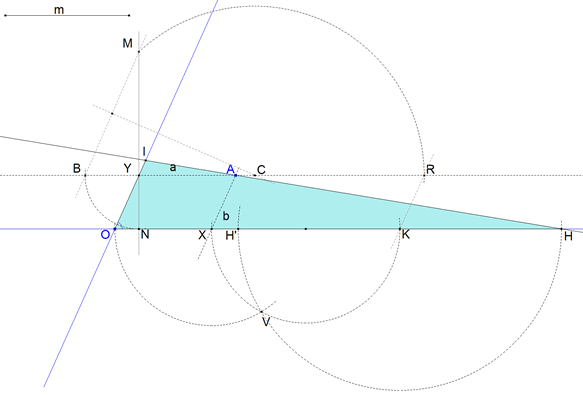
Damos dos rectas que se cortan en un punto O y damos un punto cualquiera A, una recta por A corta a las rectas dadas en H e I respectivamente (ver figura 1).

Las dos rectas dadas y la recta por A forman un triángulo OIH. El área de este triángulo es un valor dado (por ejemplo m²)

 

Tomamos las rectas dadas como ejes de coordenadas oblicuos (no rectangulares). Trazamos por A paralelas a los ejes establecidos. En estos ejes podemos escribir

.

De acuerdo con la figura 1, tomamos por ejemplo

y observando la figura 1, de nuevo, escribimos la recta IAH como

que para x=0 nos da

.

Con las expresiones de H e I entramos en la ecuación del área del triángulo

.

Para simplificar el resultado anterior, hacemos el cambio

;

geométricamente, este cambio significa transformar el cuadrado de lado m por un paralelogramo OYRK de idéntica área de lados

.

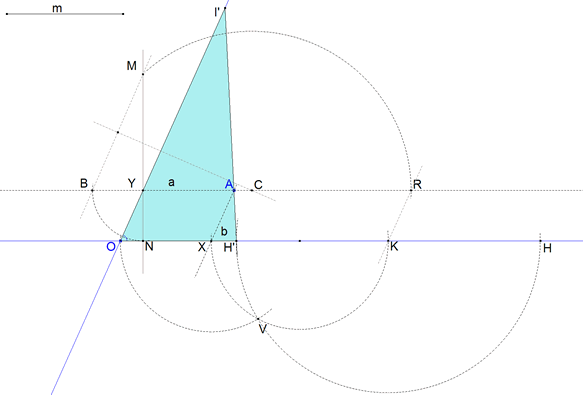
Ahora, por Y, una perpendicular a OX sobre la que, con el compás, trazamos M. YM corta a OX en N

 

,

después, por Y, una paralela a OX. Con centro en Y, un arco de radio YN que corta a la paralela en B.

 

.

La mediatriz de BM corta a BY en C. El arco de centro C y radio CM corta a BY en R. Una paralela por R a OY corta a OX en K.

 

.

BR es el diámetro del círculo con centro en C que pasa por M; ya que

 

.

 Como CM es perpendicular al diámetro

.

Por lo tanto OYRK es el paralelogramo de lados b y k con la misma área que el cuadrado de lado m. Lo anterior nos lleva a

 

cuyas soluciones son

Semicírculo de diámetro KX

.

Con centro en X, un arco de radio XO que corta al semicírculo anterior en V. Por estar sobre el semicírculo

 

.

Con centro K y radio KV arco que corta a OX en H y H’.

Una recta por H y A corta a OY en I. OIH es un triángulo de área m².

 

Una recta por H’ y A corta a OY en I’. OI’H’ es un triángulo de área m².

 

Se obtienen dos soluciones siempre que

;

pero sólo hay una solución si

y no hay ninguna solución si