 La figura de la
derecha se ha construido tomando los puntos B', A'', C'''
sobre los lados CA, BC y AB, y trazando paralelas por ellos
a los lados BC, AB y CA, respectivamente.
La figura de la
derecha se ha construido tomando los puntos B', A'', C'''
sobre los lados CA, BC y AB, y trazando paralelas por ellos
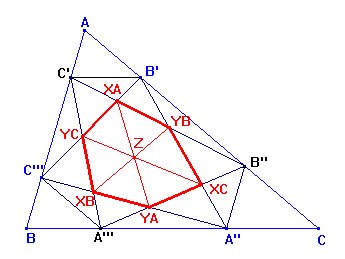
a los lados BC, AB y CA, respectivamente. | Sea ABC un triángulo. Interiormente
a él, es decir sobre los lados adyacentes a ese vértice, se
construyen los triángulos T(A)=AB'C', T(B)= BA''' C''', y T(C)= CA''B'', semejantes al triángulo dado con B' y B'' sobre AC, C' y C''' sobre AB, y A'' y A''' sobre BC, sin ser puntos medios de los lados del original ninguno de los construidos. Construimos los siguientes puntos definidos por las intersecciones de los pares de rectas que se indican: X(A) = B'C''' Ç B''C'; Y(A) = A'' C''' Ç A'''B'' ; X(B) = A'' C''' Ç C'A'''; Y(B) = A'' B' Ç B'' C'; X(C) = B'' A''' Ç A'' B', Y(C) = B'C''' Ç C'A'''. Probar que : a) Las rectas X(A)Y(A) ; X(B)Y(B) ; X(C)Y(C) son concurrentes. A partir de ahora se considera que los triángulos T(A), T(B) y T(C) tienen la misma razón de semajanza respecto a ABC. b) Las rectas X(A)Y(A) ; X(B)Y(B)
; X(C)Y(C) son concurrentes en el baricentro
de ABC. |
|
Propuesto por Juan Bosco Romero Márquez |
Solución de Francisco Javier García Capitán
 La figura de la
derecha se ha construido tomando los puntos B', A'', C'''
sobre los lados CA, BC y AB, y trazando paralelas por ellos
a los lados BC, AB y CA, respectivamente.
La figura de la
derecha se ha construido tomando los puntos B', A'', C'''
sobre los lados CA, BC y AB, y trazando paralelas por ellos
a los lados BC, AB y CA, respectivamente.
Los cálculos no son muy complicados, pero usaremos Mathematica para realizarlos:
![]()
Definimos los puntos B', A'', C''' :
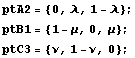
Según esta definición consideramos que BA" : A"C = 1-l :l, considerando que l = A"C:BC es la razón de homotecia de los triángulos B"A"C y ABC, y de forma análoga para los otros triángulos.
Ahora calculamos los puntos C', B" y A''', aunque también podemos deducir sus coordenadas por "simetría", teniendo en cuenta el concepto de coordenadas baricéntricas:

Hallamos los puntos de intersección XA, YB, etc.:

Tres rectas son concurrentes si el determinante de sus coeficientes es cero:
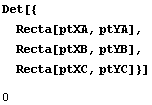
(Suponemos a partir de ahora que m =l y que n =l).
En efecto, hallamos
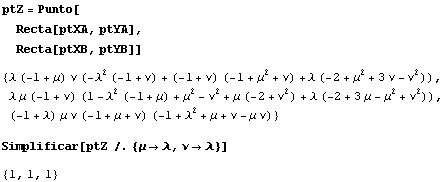
De hecho, las rectas X(A)Y(A), X(B)Y(B), X(C)Y(C) son las medianas del triángulo, que se cortan en el baricentro. Para demostrar que la recta X(A)Y(A) es la mediana correspondiente al vértice A, hacemos
![]()
y, efectivamente, la recta y = z es la mediana correspondiente al vértice A.
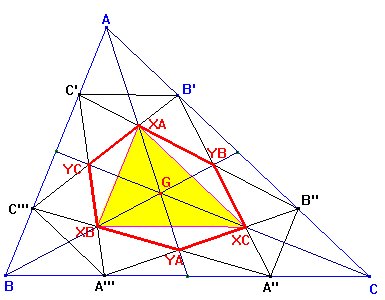 Comprobemos que
los lados de X(A)X(B)X(C) son paralelos
a los de ABC. Lo hacemos hallando el punto de intersección de
X(A)X(B) con AB y particularizando para el
caso en que l = m =
n:
Comprobemos que
los lados de X(A)X(B)X(C) son paralelos
a los de ABC. Lo hacemos hallando el punto de intersección de
X(A)X(B) con AB y particularizando para el
caso en que l = m =
n:

Al resultar un punto del infinito (la suma de sus coordenadas es cero), las dos rectas son paralelas. Lo mismo le ocurre a X(B)X(C) con BC y a X(C)X(A) con CA. Por tanto los triángulos X(A)X(B)X(C) y ABC son semejantes.
El centro de homotecia es el baricentro G del triángulo del triángulo ABC, según el apartado b).
Para hallar la razón de homotecia hacemos:
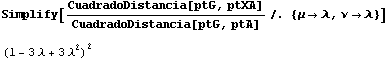
por lo que resultaque 1 - 3l + 3l2 es la razón de homotecia de los triángulos X(A)X(B)X(C) y ABC.
La expresión 1 - 3l + 3l2 decrece desde 1 (para l = 0) hasta 1/4 (para l=1/2).
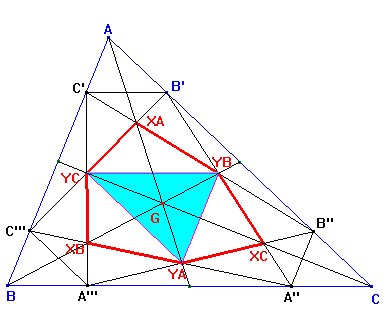 Los lados del triángulos
Y(A)Y(B)Y(C) también son paralelos
a los de ABC:
Los lados del triángulos
Y(A)Y(B)Y(C) también son paralelos
a los de ABC:

El centro de homotecia es, como antes, el baricentro G del triángulo ABC.
Para hallar la razón de homotecia hacemos:

Entonces, la razon de homotecia de los triángulos Y(A)Y(B)Y(C)
y ABC es ![]() ,
que comienza siendo 1/2 para l = 0, va decreciendo
hasta un valor mínimo de 1/3 para l = 1/3
y vuelve a crecer hasta 1/2 para l = 1/2.
,
que comienza siendo 1/2 para l = 0, va decreciendo
hasta un valor mínimo de 1/3 para l = 1/3
y vuelve a crecer hasta 1/2 para l = 1/2.
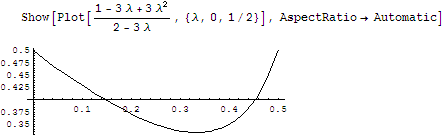
 El hexágono
A''A'''C'''C'B'B''A'' es el resultado de quitar al triángulo ABC
tres triángulos semejantes a él. Siendo l
= A"C:BC = B''C:AC, el área de B''A''C
será l2, y lo mismo la de los triángulos
BA'''C''' y AB'C'. Por tanto, el área del hexágono
A''A'''C'''C'B'B''A'' es 1-3l2.
El hexágono
A''A'''C'''C'B'B''A'' es el resultado de quitar al triángulo ABC
tres triángulos semejantes a él. Siendo l
= A"C:BC = B''C:AC, el área de B''A''C
será l2, y lo mismo la de los triángulos
BA'''C''' y AB'C'. Por tanto, el área del hexágono
A''A'''C'''C'B'B''A'' es 1-3l2.
Hagamos hicapié en que estamos considerando como unidad el área del triángulo ABC.
Para hallar el área del hexágono X(A)Y(B)X(C)Y(A)X(B)Y(C), añadimos al área D del triángulo Y(A)Y(B)Y(C) las áreas DA del triángulo X(A)Y(C)X(B), DB del triángulo X(B)Y(A)Y(C) y DC del triángulo X(C)Y(B)Y(A). Por una cuestión de simetría, estas tres áreas valen lo mismo. Entonces, para hallar el área del hexágono X(A)Y(B)X(C)Y(A)X(B)Y(C) hacemos:

La expresión que expresa el cociente de las áreas de los dos hexágonos es:
![]()
Podemos ver la variación de esta expresión en la siguiente gráfica:
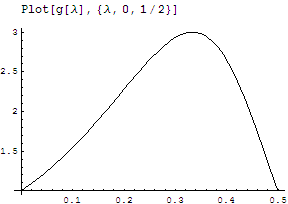
Para abreviar, diremos que el cociente de las áreas comienza siendo 1, crece, alcanzando un máximo igual a 3 para l = 1/3 y vuelve a decrecer hasta el valor inicial de 1 para l = 1/2.