Problema 257.- Sea
ABC un triángulo. Interiormente a él, es decir sobre los lados adyacentes a ese
vértice, se construyen los triángulos T(A)=AB'C', T(B)=
BA'''C''', y T(C)= CA''B'', con B' y B'' sobre AC, C' y C''' sobre AB, y
A'' y A''' sobre BC, sin ser puntos medios ninguno de los construidos semejantes
al triángulo dado.
Construimos los siguientes puntos definidos por las intersecciones de
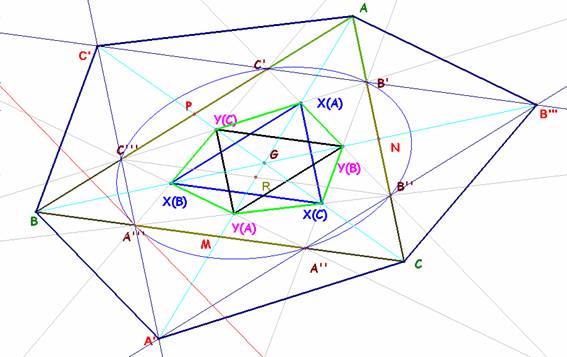
los pares de rectas que se indican: X(A)= B'C''' Ç B''C'; Y(A) = A''
C''' Ç A'''B'' ; X(B) = A'' C''' Ç C'A'''; Y(B) = A''
B' Ç B'' C'; X(C) = B'' A''' Ç A'' B', Y(C)
= B'C''' Ç C'A'''.
Probar
que:
a) Las rectas X(A)Y(A) ;
X(B)Y(B) ; X(C)Y(C) son concurrentes.
A partir de ahora se considera que los triángulos T(A), T(B)
y T(C) tienen la misma razón de semejanza respecto a ABC.
b) Las rectas X(A)Y(A) ; X(B)Y(B) ; X(C)Y(C)
son concurrentes en el baricentro de ABC.
c) Probar que los triángulos X(A)X(B)X(C),
Y(A)Y(B)Y(C) y ABC son semejantes, y encontrar su centro y razón de homotecia.
d)Calcular la razón de las áreas de los hexágonos
A''A'''C'''C'B'B''A'' y X(A)Y(B)X(C)Y(A)X(B)Y(C).
Propuesto por Juan
Bosco Romero Márquez, profesor colaborador de
Solución de
Saturnino Campo Ruiz, profesor del IES Fray Luis de León de Salamanca.
a) Para esta
primera parte consideraremos los siguientes resultados en los que vamos a
apoyarnos para la demostración.
·
Teorema 1 (de Pascal.)- La
condición necesaria y suficiente para que un hexágono esté inscrito en
una cónica es que estén alineados los puntos de corte de los pares de lados
opuestos (demostrado
en el problema 216)
·
Teorema 2 (de Brianchon).- La condición necesaria y suficiente para
que un hexágono sea tangente a una cónica es que sean concurrentes las
rectas que unen los pares de vértices opuestos. (dual del anterior, que
usaremos sin demostrar)
·
Teorema. 3- Si los seis vértices de dos
triángulos están sobre una cónica, los seis lados de los triángulos son
tangentes a otra cónica y viceversa.(Utilizado y demostrado en la resolución del
problema nº 182 de los polígonos cerrados de Poncelet)
El hexágono C’ C’’’ A’’’ A’’ B’’ B’ tiene sus lados opuestos paralelos, por tanto
se cortan en puntos de la misma recta ─la recta del infinito─ y
según el teorema 1 (de Pascal) hay una cónica que pasa por ellos.
Con los vértices de este hexágono pueden construirse
dos triángulos: A’’’ B’’ C’ y A’’
B’ C’’’ inscritos en la cónica
anterior; según el teorema 3, sus lados son tangentes a otra cónica. Esta
cónica es la inscrita en el hexágono de vértices X(A)Y(B)X(C)Y(A)X(B)Y(C).
El teorema 2 (de Brianchon) nos asegura que los
vértices opuestos de este hexágono, concurren en un punto ( K en el dibujo) y con esto concluimos esta
primera parte.
b) Si
los triángulos construidos en las esquinas del triángulo principal son
iguales, la situación cambia: Prolongando los lados A’’’ C’’’ y A’’
B’’ obtenemos el punto A’ que junto con B’’, A y C’’’
determina un paralelogramo. Sus diagonales son la mediana desde A y el
segmento C’’’ B’’ paralelo a la base BC, que se cortan en el
punto R, centro del mismo. El punto A’ se obtiene por simetría
del punto A respecto de R y por tanto, los triángulo A’ B’’
C’’’ y A B’’ C’’’ son
iguales.
Los segmentos A’’’ A’’ y C’B’ son paralelos a la base C’’’ B’’ y por esa razón los puntos X(A)
e Y(A) están sobre las medianas desde A y A’ respectivamente, que, como puede
verse es la diagonal AA’ del paralelogramo. Por tanto los puntos X(A) e Y(A)
están sobre la mediana trazada desde A (demostrado en el problema nº 68).
El resto es trivial.
c) Prolongando también el segmento C’B’
obtenemos un nuevo triángulo A’B’’’C’’ de lados paralelos a ABC
y, por tanto, semejante a él. Sus lados miden 2a─ 3a’, 2b
─ 3b’y 2c─3c’ respectivamente. Lo
llamaremos T(A’). La razón de semejanza con ABC es 2─3 k siendo k = a’/a = b’/b = c’/c.
Los seis vértices de estos dos triángulos forman un
hexágono H’=AB’’’CA’BC’’.
1.-El hexágono AB’’’CA’BC’’ es
semejante al hexágono H(X,Y)= Y(A)X(B)Y(C)X(A)Y(B)X(C).
·
La existencia del paralelogramo A’B’’AC’’’ nos permite concluir
que los triángulos A’A’’C y BA’’’A’ son
respectivamente iguales a los triángulos C’’’C’B’ y C’B’B’’ y por ello los segmentos
Y(C)X(A) y X(A)Y(B)
son paralelos a CA’ y A’B respectivamente.
·
Idénticos razonamientos con los paralelogramos BC’B’’’A’’ y
C’’A’’’CB’ completan la demostración de la semejanza.
2.- En esta semejanza la correspondencia de vértices
homólogos es la siguiente:
(A’, B’’’, C’’, A, B, C) ßà ( X(A), X(B),
X(C), Y(A), Y(B), Y(C) )
y de ella puede concluirse que los triángulos T(X)
= X(A)X(B)X(C) y T(Y)= Y(A)Y(B)Y(C)
son respectivamente semejantes a T(A’)
= A’B’’’C’’ y a ABC, y en
definitiva, ambos son semejantes a ABC como se pretendía demostrar.
3.- De la parte b) se sigue que el centro de
la homotecia que transforma un hexágono en el otro es el baricentro del
triángulo ABC. La razón de
esta homotecia es negativa (basta observar la orientación de los segmentos
homólogos).
Prescindiendo del signo vamos
a llamar x a la razón de homotecia de
los triángulos ABC y T(X) e y a la de ABC y T(Y)
(que es la misma que la de los triángulos T(A’) y T(X)).
La relación entre éstas es la
siguiente:
y2 = 
= (2-3k)2·x2.
Esto es, y = (2
─ 3k)·x
4.-Para calcular la razón de homotecia, después de
estas consideraciones, nos fijamos en el triángulo AGN cortado por la transversal B’’C’. La
aplicación del teorema de Menelao nos da el siguiente producto de razones
simples:
( X(A) G A) · ( B’’ A N)
· ( Y(B) N G) = 1
G también es el
baricentro T(X) y T(Y), por ello, x = 
e y =
y de aquí
= x – 1; 
= 1/2·y
─ 1
( B’’ A N ) = 
.
Despejando de la relación obtenida con el teorema de
Menelao resulta:
( X(A) A G) = ( B’’ A N)
· ( Y(B) N G)
Sustituyendo en ella se tiene el sistema:
x ─ 1 = ( y
─2)· 
y = (2─3k)x
Resolviéndolo con paciencia, se obtienen:
1/x =3k2 ─ 3k +
1 que es la
razón de semejanza de T(X) a ABC y
1/y = 
que es la razón de semejanza de T(Y)
a ABC.
Y con esto se concluye la parte c).
d) La razón de semejanza del hexágono AB’’’CA’BC’’ al
hexágono H(XY)
es la de ABC con T(Y),
o sea
y = 
Para hallar la
razón de áreas pedidas vamos a calcular el área del hexágono H’ = AB’’’C....
Como resulta evidente de la observación de la figura,
esa área es igual a la del triángulo T(A‘) más las áreas de los
triángulos construidos exteriormente sobre cada lado, de vértices A, B y
C.
Estos tres triángulos tienen igual área: [AB’B’’’ ]
= [C’’C’A] y [AB’B’’’ ] = [B’’’B’’C ] por
tener iguales, en cada caso, una base y una altura.
Hay que calcular el área de uno de ellos, sea AB’B’’’,
en función del área de ABC.
La razón del área de AB’B’’’ con AB’C’ es (a –2a’ )/a’
= 
por tener la misma altura.
La razón del área de AB’C’ con ABC es k2
y por tanto la razón del área de AB’B’’’ con ABC es el
producto de esas dos expresiones, o sea,
k(1 ─ 2k).
Tenemos pues
Area(C’’AB’’’) = k(1─2k) + k(1─2k)+
k(1 ─ 2k) · Area(ABC).= (2k ─ 3k2)·Area(ABC).
Ya habíamos calculado Area(T(A’)) = (2 ─ 3k)2
·Area(ABC). Uniendo todo resulta:
Area(H’) = [ (2 ─
3k)2 + 3·(2k ─ 3k2)
]·Area(ABC) = (4 ─ 6k) ·Area(ABC) .
Aplicando la razón de semejanza entre los hexágonos tendremos:
Area(H(XY))=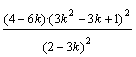
·Area(ABC)= 
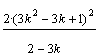·Area(ABC).
El hexágono inscrito en ABC tiene área igual a la de éste menos 3
veces el área del triángulo AB’C’.
Area(B’C’C’’’A’’’A’’B’’)
= (1 ─ 3k2) ·Area(ABC). Finalmente, la
razón entre las áreas que se busca es
l = 
.