Problema 258

Demostrar que si el ángulo A de un triángulo ABC vale 60º, la recta que une el ortocentro con el centro del círculo circunscrito forma con los lados AB y AC, un triángulo equilátero.

Matemática Elemental (1933): Tomo II, N.3, página 49.
Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid.

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba, España.

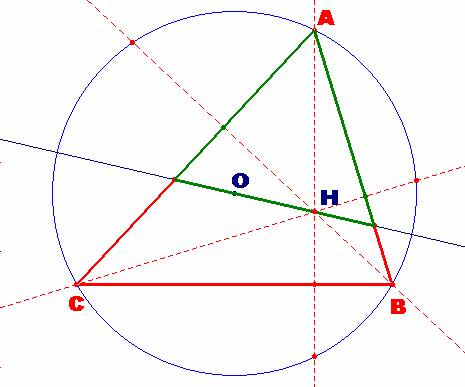
Dado el triángulo ABC, con el ángulo A=60º, construimos el punto H, ortocentro del mismo y el centro O de la circunferencia circunscrita.

Veamos que, en efecto, la recta OH determina con los lados AB y AC un triángulo equilátero (dibujado en verde).

Para ello, tengamos en cuenta los siguientes hechos de interés:

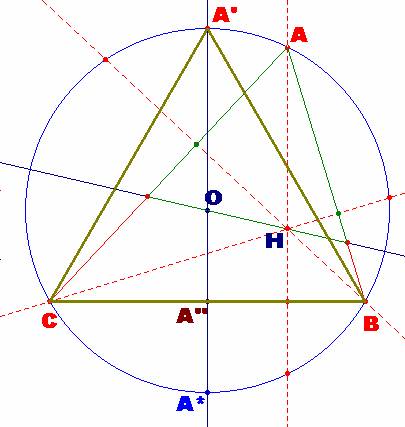
1.- Siendo A’’ el punto medio del lado BC y A* el punto donde la mediatriz del lado BC corta a la circunferencia circunscrita al triángulo ABC, tenemos que:
A’’ es el punto medio del segmento OA*.

Esto es cierto ya que al considerar el triángulo equilátero A’BC ,vemos que los puntos O, A’’ y A* no cambian y así en este triángulo OA’=2∙OA’’, pero OA’= OA*= R (radio de la circunferencia).

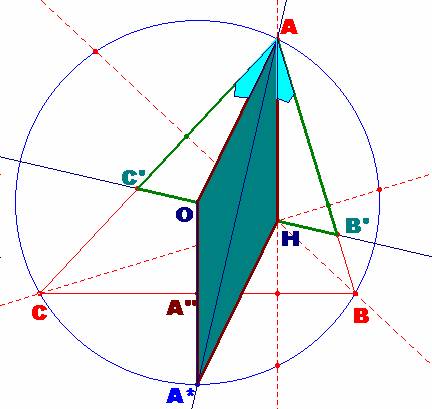
2.- Sabemos que, en general, el segmento AH = 2∙OA’’. En este caso en particular, tendremos que AH = R. Por otra parte, OH es paralelo al segmento OA*, por ser ambos perpendiculares al lado BC. Entonces podemos considerar el rombo de vértices OA*HA de lado igual a R. Como quiera que A* es el pie de la bisectriz AA* del ángulo en A, también lo será de los lados AO y AH del rombo.
Esto último querrá decir que los ángulos <OAC’ = < HAB’ serán iguales. Como ya lo eran los ángulos exteriores al rombo en los vértices O y H, concluimos que los ángulos en B’ y C’ son iguales, siendo así el triángulo AB’C’ equilátero, c.q.d.