Problema 258

Propuesto por Juan Bosco Romero Márquez,

profesor colaborador de la Universidad de Valladolid

Problema 73.
Demostrar que si el ángulo A de un triángulo ABC vale
60, la recta que une el ortocentro con el centro del cículo
circunscrito forma con los lados AB y AC, un triángulo equilátero.
Matemática Elemental (1933): Tomo II, N.3, página 49

Solución del editor

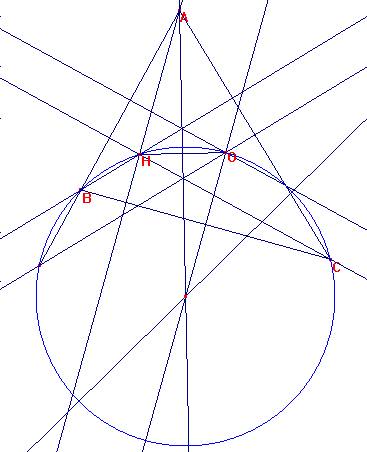
Sean <BAC=60, <ABC=60+b, <ACB=60-b.

Es <HBC=90-<ACB=90-(60-b)=30+b

<HCB=90-<ABC=90-(60+b)=30-b.

<BHC=180-(30-b)-(30+b)=120

Al ser O el circuncentro, es <BOC=2*<BAC=120.

Luego BHOC es un cuadrilátero circunscrito.

Al ser AH perpendicular a BC, es: <HAB=90-(60+b)=30-b.

Al ser BOC isósceles, es <OBC=30, con lo que <ACO=<CAO=30-b.

Así, <HAO=<BAC-<HAB-<CAO=60-(30-b)-(30-b)=2b.

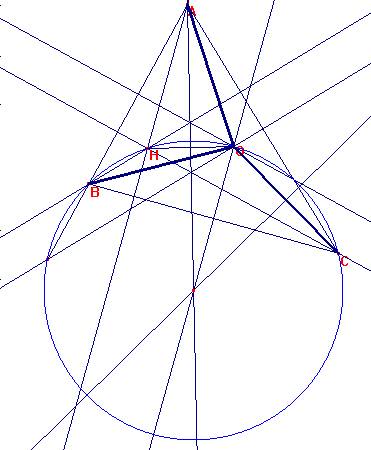
Es <AOC=180-<ACO-<CAO=180-(30-b)-(30-b)=120+2b.

<BOC=120.

HOB=<HCB=30-b.

Luego es <AOH=360-<AOC-<COB-HOB= 360-(120+2b)-(120)-(30-b)=90-b.

Luego se tiene que <AHO=180-<HAO-<AOH=180-2b-(90-b)=90-b.

AHO es por tanto isósceles.

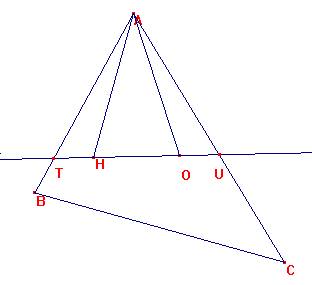
Consideremos la recta que pasa por HO.

Corta a AB en T, y a AC en U.

En el triángulo AHT es : <TAH=30-b, <AHT=90+b, por lo que <ATH=60.

Así, ATU es equilátero, cqd.

Ricardo Barroso Campos

Didáctica de las Matemáticas

Universidad de Sevilla.