Problema 258
Propuesto por Juan Bosco Romero Márquez,
profesor
colaborador de
Problema 73.
Demostrar que si el ángulo A de un triángulo ABC vale
60, la recta que une el ortocentro con el centro del
círculo
circunscrito forma con los lados AB y AC, un triángulo equilátero.
Matemática Elemental (1933): Tomo II, N.3, página 49
Solución
de
Maite Peña
Alcaraz, estudiante de Industriales en
:
 Podemos
suponer sin pérdida de la generalidad que
Podemos
suponer sin pérdida de la generalidad que ![]() . El caso de la igualdad podemos omitirlo porque coinciden el
ortocentro y el cicuncentro.
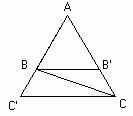
En los demás casos, sea B’ un punto sobre AC tal que ABB’ sea un triángulo
equilátero y sea C’ un punto sobre la recta AB de tal modo que ACC’ sea también
un triángulo equilátero. Entonces, el ortocentro será
la intersección de la recta perpendicular a AC que pasa por el punto medio de
AB’ y la recta perpendicular a AB que pasa por el punto medio de AC’. El circuncentro es la intersección de la recta perpendicular a
AC que pasa por el punto medio de AC y la recta perpendicular a AB que pasa por
el punto medio de AB, y como AB=AB’ y AC=AC’, HO es paralela a BB’ y CC’ y por
tanto el triángulo que forma con las rectas AB y AC es equilátero.
. El caso de la igualdad podemos omitirlo porque coinciden el
ortocentro y el cicuncentro.
En los demás casos, sea B’ un punto sobre AC tal que ABB’ sea un triángulo
equilátero y sea C’ un punto sobre la recta AB de tal modo que ACC’ sea también
un triángulo equilátero. Entonces, el ortocentro será
la intersección de la recta perpendicular a AC que pasa por el punto medio de
AB’ y la recta perpendicular a AB que pasa por el punto medio de AC’. El circuncentro es la intersección de la recta perpendicular a
AC que pasa por el punto medio de AC y la recta perpendicular a AB que pasa por
el punto medio de AB, y como AB=AB’ y AC=AC’, HO es paralela a BB’ y CC’ y por
tanto el triángulo que forma con las rectas AB y AC es equilátero.