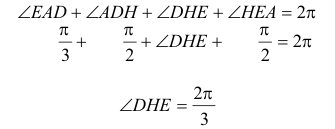Problema 258
Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid
Problema 73. Demostrar que si el ángulo A de un triángulo ABC vale 60, la recta que une el ortocentro con el centro del círculo circunscrito forma con los lados AB y AC, un triángulo equilátero.
Matemática Elemental (1933): Tomo II, N.3, página 49
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (7 de julio de 2005) |
|
¿DÓNDE ESTÁ EL VÉRTICE A Y EL CIRCUNCENTRO O DEL TRIÁNGULO? |
|
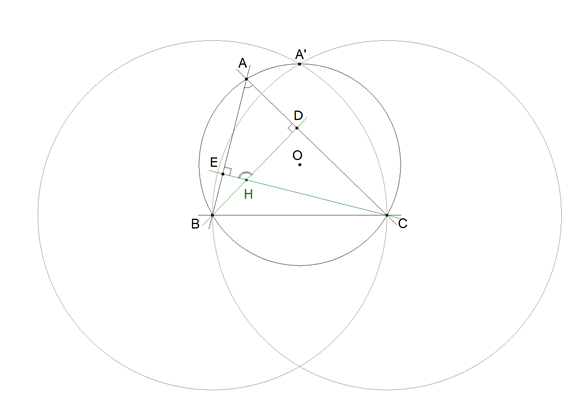
El ángulo A es siempre de 60º (π/3). Fijada la base BC, el lugar geométrico de A será entonces el arco capaz de ángulo π/3 y cuerda BC; Como B, C y A pertenecen a ese arco capaz y ABC están sobre su circunferencia circunscrita:
DETERMINAMOS QUE EL LUGAR GEOMÉTRICO DEL VÉRTICE A ES LA CIRCUNFERENCIA CIRCUNSCRITA A LOS TRIÁNGULOS ABC, ESA CIRCUNFERENCIA ES FIJA YA QUE B Y C PERTENECEN A ELLA Y A LA RECORRE. POR SER LA CIRCUNFERENCIA CIRCUNSCRITA FIJA, EL CIRCUNCENTRO O TAMBIÉN ES FIJO. 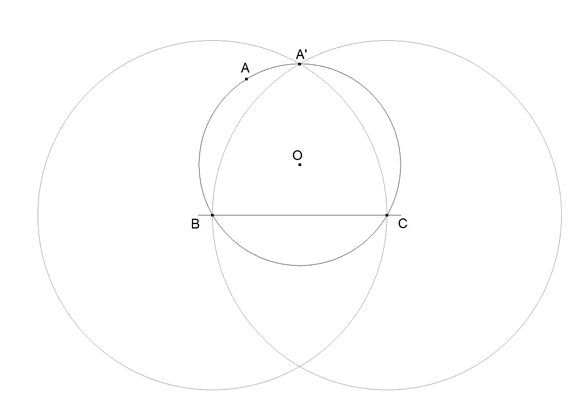 figura 1 La determinación más fácil nos la proporciona el triángulo equilátero A’BC; luego cualquier punto A sobre el círculo circunscrito puede ser vértice del triángulo ABC con ángulo π/3. Trazamos una recta cualquiera BC como base de la familia de triángulos que nos dice el enunciado. Con centro en B, círculo de radio BC. Con centro en C, círculo de radio CB. Estos dos círculos se cortan en A’. A’BC es equilátero. El círculo circunscrito a A’BC es el lugar de los vértices A con ángulo en A π/3.
|
|
EL ORTOCENTRO H Y EL ÁNGULO DHE |
|
La perpendicular por B a CA corta esta última en D. La perpendicular por C a AB corta esta última en E.
figura 2
|
|
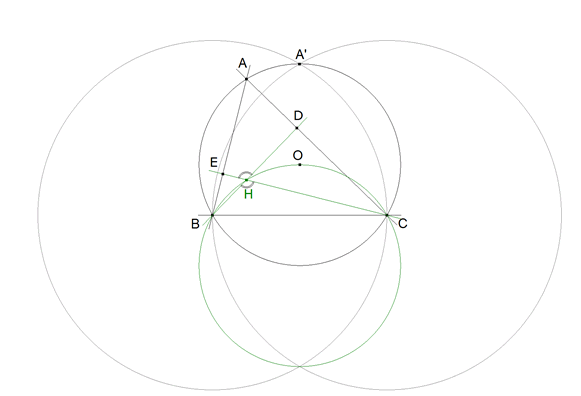
EL LUGAR GEOMÉTRICO DEL ORTOCENTRO H |
|
figura 3
|
|
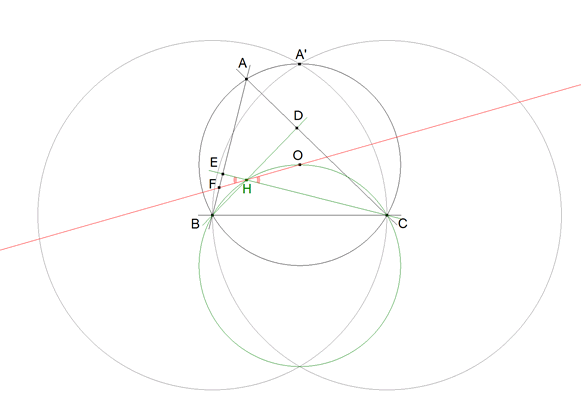
LA RECTA POR OH Y SU ÁNGULO CON AB Y CA |
|
|
La recta OH corta al lado AB en F; ello implica que debemos determinar el ángulo HFE.
figura 4 Pero O y C son fijos sobre el círculo BCO y H está sobre ese círculo, entonces el ángulo CHO corresponde al arco OC y por tanto será fijo.
LOS TRES ÁNGULOS DEL TRIANGULO QUE FORMA LA RECTA POR EL ORTOCENTRO Y EL CIRCUNCENTRO CON LOS LADOS AB Y CA DEL TRIÁNGULO ABC SON IGUALES A Π/3 Y POR TANTO EL TRIÁNGULO ES EQUILÁTERO.
|