Problema 258

Problema 258

Propuesto por Juan Bosco Romero Márquez,

Profesor colaborador de la Universidad de Valladolid

Problema 73.
Demostrar que si el ángulo A de un triángulo ABC vale
60, la recta que une el ortocentro con el centro del círculo
circunscrito forma con los lados AB y AC, un triángulo equilátero.
Matemática Elemental (1933): Tomo II, N.3, página 49

Solución del Prof. William Rodríguez Chamache

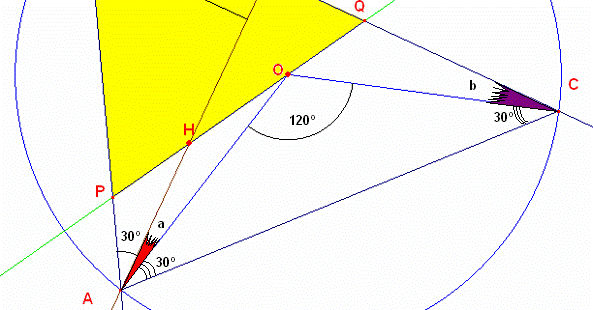
Partimos de la siguiente gráfica donde demostraremos que el triángulo PBQ es equilátero

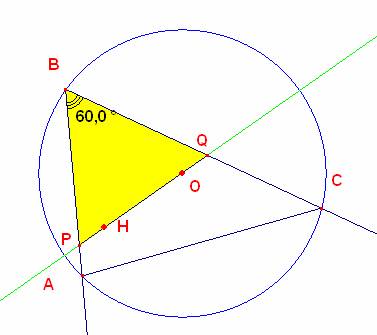
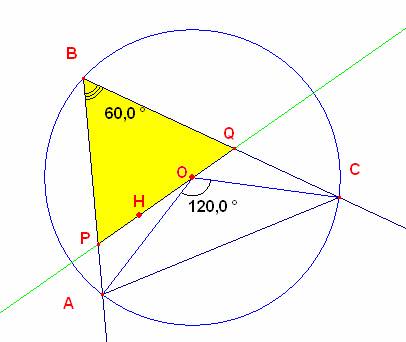
Unimos OA y OC que son iguales por ser O el circuncentro luego el ángulo AOC=120º

También observamos que el ángulo BAH=30º pues observamos que AH es perpendicular a BC.

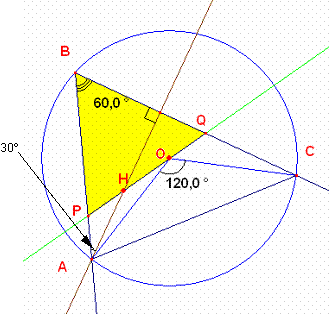
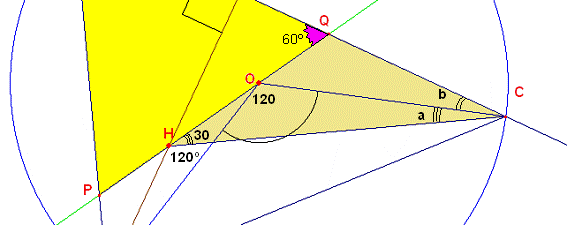
Luego observando la figura vemos que: a+b=30º

Pero al unir CH se determina los , por lo tanto el ángulo AHC=120º por lo que se demuestra que el cuadrilátero AHOC es inscriptible.

Por lo tanto el ángulo OHC=30º y el ángulo HCO=a

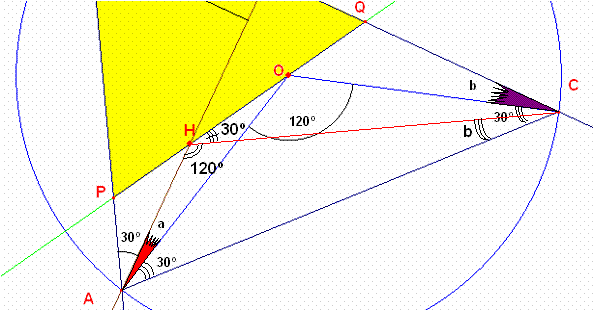
Finalmente en el triángulo HQC por propiedad del ángulo externo se sabe que Q=60º finalmente queda demostrado que el triángulo PAQ es equilátero