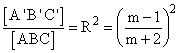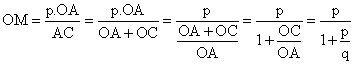Problema 259

Sobre los lados de un triángulo ABC se dan pares de puntos A1-A2, B1-B2, C1-C2, tales que
A1B/A1C=A2C/A2B=B1C/B1A=B2A/B2C=C1A/C1B=C2B/C2A=m.
Hallar la razón de áreas entre el triángulo dado y el que tiene por vértices los puntos siguientes:
A´= BB1 intersección CC2,
B´= CC1 intersección con AA2,
C´= AA1 intersección BB2.

Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid. Matemática Elemental, (1941): N.2, páginas 69-70.

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba, España.

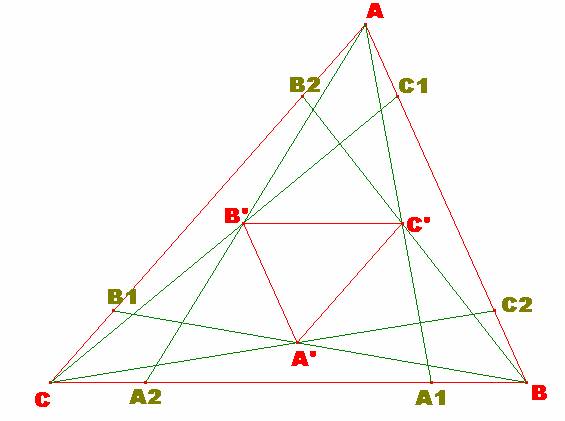
Supongamos que el parámetro m<1. De esta manera tendremos la siguiente configuración del triángulo ABC

Convendrá, antes de continuar, destacar algunos hechos de interés:

1.- La recta AA' pasa por el punto medio del lado BC.
Esto es evidente sin más que considerar en el trapecio de bases BC y C₂B₁ sus diagonales correspondientes y notar que se cortan en el punto A'.
(Ver para más detalle el siguiente ejercicio).

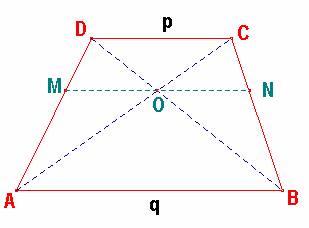
Ejercicio.
Hallar la longitud del segmento de la recta paralela a las bases del trapecio, la cual pasa por el punto de intersección de las diagonales, si las bases del trapecio son p y q.

De la semejanza de los triángulos AOB y COD, obtenemos:

De la semejanza entre los triángulos AOM y ACD, obtenemos: .
De esta última igualdad deducimos que:

En definitiva,

De igual modo, obtendríamos que: .
Por fin, tendremos que:
.

Volviendo de nuevo a nuestro problema, tenemos que mutatis mutandi los puntos B' y C' pertenecen igualmente a las medianas m_b y m_c, respectivamente.

Si probáramos la existencia de una homotecia de centro el punto G, baricentro del triángulo ABC, que transformase el triángulo ABC en el A'B'C', entonces la razón de las áreas sería, sin más, que el cuadrado de la razón de semejanza entre aquellos triángulos.
Para ello, veamos qué ocurre con el punto A'.

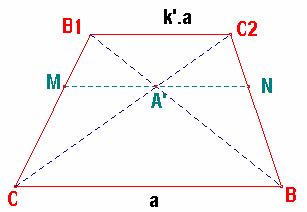En el trapecio ABC₂B₁, de bases a y k’×a, respectivamente, tenemos que:

Usando la notación del enunciado inicial: .




Luego la anterior expresión quedaría de la forma:

Así tendremos que:

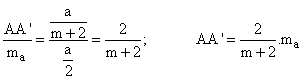
Como GA=2/3×m_a , entonces el punto G se encuentra entre A y A' ya que , como ya se había advertido en el convenio inicial.
De esta forma, GA' = AA'-GA;
Luego entonces:
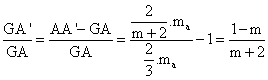, razón que depende únicamente del parámetro m.
Por tanto y de igual manera tendríamos que: .
Y así tenemos que el triángulo A'B'C' sería el transformado del ABC por la homotecia de centro el punto G y de razón negativa .
Por tanto, la razón de áreas entre ambos triángulos será igual a R².